MatheAss 10.0 − Algebra lineare
Sistemi delle equazioni lineari
Il programma determina il vettore della soluzione da un sistema di equazioni lineari con n equazioni e n incognite.
Esempio: Cercando una parabola attraverso i punti P(1|3), Q(2|1) e R(4|9) si arriva al sistema di equazioni.
1·x1 + 1·x2 + 1·x3 = 3
4·x1 + 2·x2 + 1·x3 = 1
16·x1 + 4·x2 + 1·x3 = 9
L = (2; -8; 9)
La parabola ha quindi l'equazione y = 2x 2 - 8x + 9.
Esempio con una soluzione bidimensionale:
0·x1 + 0·x2 + 2·x3 - 1·x4 = 1
1·x1 + 1·x2 + 1·x3 + 1·x4 = 4
2·x1 + 2·x2 - 4·x3 + 5·x4 = 5
1·x1 + 1·x2 - 7·x3 + 5·x4 = 0
L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }
Ottimizzazione lineare
( Nuovo nella versione 9.0 da febbraio 2022 )
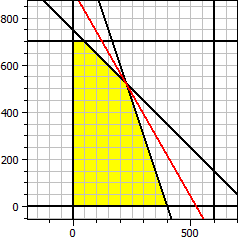
Il programma determina la soluzione ottimale per una funzione obiettivo a due variabili con disuguaglianze lineari come vincoli.
Funzione obiettivo: ƒ(x,y) = 140·x + 80·y → Maximum Vincoli: x ≥ 0 y ≥ 0 x ≤ 600 y ≤ 700 x + y ≤ 750 3·x + y ≤ 1200 Massimo x = 225 y = 525 ƒ(x,y) = 73500
Combinazione lineare
Il programma determina la combinazione lineare di un vettore da tre vettori dati. La routine è adatta anche per verificare l'indipendenza lineare di tre vettori nello spazio, cioè se giacciono su un piano.
⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 2 ⎫
a·⎪ 0 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪
⎩ 0 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭ ⎩ 4 ⎭
Solution:
a = -1 b = -1 c = 4
Prodotto scalare
Il programma calcola il prodotto scalare di due vettori, la lunghezza dei due vettori e l'angolo racchiuso.
-> ⎧ 1 ⎫ -> ⎧ 5 ⎫
a = ⎪ 3 ⎪ b = ⎪ 0 ⎪
⎩ 1 ⎭ ⎩ 3 ⎭
Prodotto scalare = 8
Lunghezza del 1° vettore = √11 = 3,32
Lunghezza del 2° vettore = √34 = 5,83
Angolo incluso α = 65,56°
Prodotto vettoriale
Il programma calcola il prodotto vettoriale e la sua valore assoluto per due vettori. Il prodotto vettoriale è perpendicolare al parallelogramma percorso da te e la sua valore assoluto è uguale all'area del parallelogramma.
-> ⎧ 1 ⎫ -> ⎧ 7 ⎫
a = ⎪ 2 ⎪ b = ⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 4 ⎭
-> -> ⎧ 5 ⎫ -> ->
a x b = ⎪ 17 ⎪ |a x b|= √483 = 21,977261
⎩-13 ⎭
Prodotto misto
Il programma calcola il prodotto misto per tre vettori. La sua valore assoluto indica il volume del cuboide spostato (spatola) che è attraversato dai tre vettori.
-> ⎧ 2 ⎫ -> ⎧ 2 ⎫ -> ⎧ 3 ⎫
a = ⎪ 3 ⎪ b = ⎪-1 ⎪ c = ⎪ 9 ⎪
⎩ 5 ⎭ ⎩ 7 ⎭ ⎩ 2 ⎭
-> -> ->
( a x b ) · c = 26
Inversione di una matrice
Il programma calcola il determinante, il rango e la matrice inversa per una matrice quadrata di ordine n.
Matrice : ¯¯¯¯¯¯¯¯ ⎧ 1 0 2 ⎫ ⎪ 0 1 0 ⎪ ⎩ 3 0 1 ⎭ Matrice inversa : ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧-0,2 0 0,4 ⎫ ⎪ 0 1 0 ⎪ ⎩ 0,6 0 -0,2 ⎭ Ordine = 3, Rango = 3, Determinante = -5
Matrice pseudo-inversa
Se le colonne di una matrice A sono linearmente indipendenti, allora
A+ = ( AT· A )-1· AT
A+ è un inverso sinistro di A , ciò significa che si applica:
Matrice A ¯¯¯¯¯¯¯¯¯ ⎧ 1 1 1 1 ⎫ ⎩ 5 7 7 9 ⎭ AT· A ¯¯¯¯¯ ⎧ 26 36 36 46 ⎫ ⎪ 36 50 50 64 ⎪ ⎪ 36 50 50 64 ⎪ ⎩ 46 64 64 82 ⎭ AT· A non invertibile A · AT ¯¯¯¯¯¯ ⎧ 4 28 ⎫ ⎩ 28 204 ⎭ ( A · AT )-1 ¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 6,375 -0,875 ⎫ ⎩-0,875 0,125 ⎭ Right Inverse: AT·( A·AT )-1 ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 2 -0,25 ⎫ ⎪ 0,25 0 ⎪ ⎪ 0,25 0 ⎪ ⎩ -1,5 0,25 ⎭
Moltiplicazione delle matrice
Il programma calcola il prodotto per due matrici.
1° matrice: ¯¯¯¯¯¯¯¯¯¯¯ ⎧ 1 0 2 ⎫ ⎩ 0 1 0 ⎭ 2° matrice: ¯¯¯¯¯¯¯¯¯¯¯ ⎧-0,2 0 0,4 1 ⎫ ⎪ 0 1 0 1 ⎪ ⎩ 0,6 0 -0,2 1 ⎭ Prodotto di matrici: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 1 0 0 3 ⎫ ⎩ 0 1 0 1 ⎭
