MatheAss 10.0 − Geometria 2D

Triangoli rettangoli

Dati due degli elementi di un triangolo rettangolo gli altri sono calcolati./p> 

Dato:
¯¯¯¯
 Segmento di ipot. p = 1.8
                    Area  A = 6 
 
Risultati:
¯¯¯¯¯¯¯
                  Cateto a = 3 
                  Cateto b = 4
	     Ipotenusa c = 5				  
                 Angolo α = 36.869898°
                 Angolo β = 53,130102°
Segmento di ipot. q = 3,2
                Altezza h = 2,4

Triangoli da tre elementi

Se si immettono 3 elementi esterne di un triangolo (lati o angoli) il programma calcola gli altri lati, angoli, altezze, mediane, bisettrici, circonferenza e area. Inoltre, il centro e il raggio del cerchio inscritto e il cerchio circoscritto. Inoltre, vengono disegnati triangoli con cerchi inscritti e circoscritti.

Dato: a=6, b=4  e  α=60°

           Vertici:   A(1|1)         B(7,899|1)   C(3|4,4641)
               Lati:   6                4                  6,89898
           Angoli:   60°             35,2644°     84,7356° 
         Altezze:   3,98313      5,97469      3,4641 
       Mediane:   4,77472      6,148          3,75513
      Bisettrici :   4,38551      6,11664      3,5464

Circumcerch.:   M(4,44949|1,31784)       ru = 3,4641
     Incerchio :  O(3,44949|2,41421)        ri = 1,41421

       Area: A = 11,9494        Perimetro :  u = 16,899
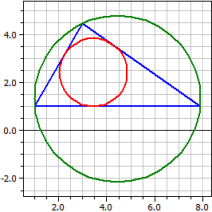
Triangle

Triangoli di 3 punti

Dalle coordinate di tre vertici, il programma calcola tutte le quantità esterne ed interne (vedi triangoli di tre dimensioni).

           Vertici :  A(1|0)          B(5|1)          C(3|6) 
	  
               Lati :  5,38516       6,32456       4,12311
           Angoli :  57,5288°     82,2348°     40,2364° 
         Altezze :  4,0853         3,47851       5,33578
      Mediane :  4,60977       3,60555       5,5 
      Bisettrici :  4,37592       3,51849       5,46225 

Circumcerch.:  M(2,40909|2,86364)     ru = 3,19154
     Incerchio :  O(3,11866|1,96195)      ri = 1,38952
   
      Area :  A = 11            Perimetro : u = 15,8328

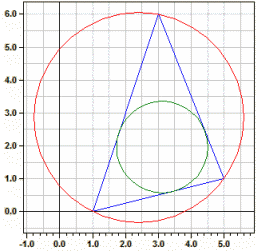
Linee speciali nel triangolo   (nuovo nella versione 9.0)

Il programma calcola le equazioni delle asse dei lati, delle mediane, delle bisettrici e delle altitudini di un triangolo.
Inoltre, i centri e i raggi del circumcerchio, del incerchio dei tre excerchi e del cerchio di Feuerbach (da marzo 2025).

Dato:  
¯¯¯¯      
          Vertici: A(1|0)  B(5|1)  C(3|6)
     
Risultati:       
¯¯¯¯¯¯¯  
          Lati: a:  5 · x + 2y = 27       
                  b:  3x - y = 3       
                  c:  x - 4y = 1     
	       
Incerchio: Mi(3.119|1.962)    ri = 1.390
	    
Excerchi: Ma(7.626|6.136)   ra = 4.346
                Mb(-4.356|5.784)  rb = 6.910
                Mc(3.248|-2.427)  rc = 2.900

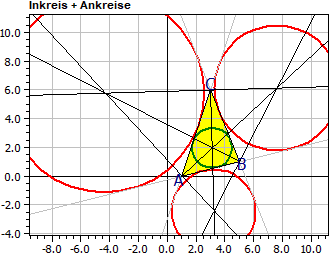
Poligoni regolari

Considerato uno dei seguenti elementi di un poligono con n vertici, gli altri sono calcolati:
Side, raggio circolo circoscritta, raggio circolo inscritto, perimetro o area.

Dato:  
¯¯¯¯ 
              Vertici n = 6
Circumcerchio rc = 1
  
Risultati:  
¯¯¯¯¯¯¯
               Lato   a = 1
     IncCerchio   ri = 0,8660254
        Perimetro  p = 6
                Area  A = 2.5980762

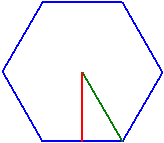
Poligoni arbitrari

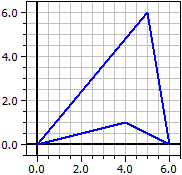
Dalle coordinate dei vertici di un poligono, il programma calcola l'area, la circonferenza e le coordinate dei centri di gravità (rispettivamente nei punti o nell'area) e viene disegnato il poligono.

Vertici:       Area  A = 18
 A (0 | 0)     
 B (4 | 1)   Circonferenza p = 22.032567
 C (6 | 0)     
 D (5 | 7)   Baricentro di vertici:
                 CP (3,75 | 2)
            
                 Baricentro di area:
                 CA (3,72,222 mila | 2.66667)

Trasformationi dei poligoni   (revisto nella versione 9.0)

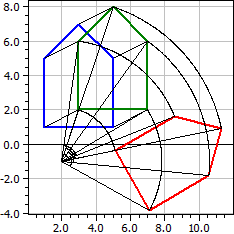
Il programma permette di applicare una concatenazione di trasformationi ad un poligono. È possibile scegliere tra traslazione, riflessione diritta, riflessione puntuale, rotazione, dilatazione centrico e trasformatione di taglio.

Poligono originale
A(1|1), B(5|1), C(5|5), D(3|7), E(1|5), 

1. Traslazione: dx=2, dy=1  ☑
A(3|2), B(7|2), C(7|6), D(5|8), E(3|6), 

2. Rotazione: Z(2|-1), α=-60° ☑
A(5,0981|-0,36603), B(7,0981|-3,8301),
C(10,562|-1,8301), D(11,294|0,90192),
E(8,5622|1,634),

Cerchi e sue parti

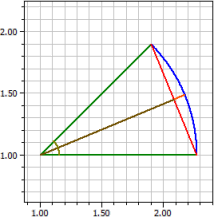
Dati due elementi di un settore circolare, raggio, angolo, arco, corda, sezione, segmento, area, perimetro, distanza tra corda e ad arco e la freccia altezza sono calcolate.

Dato:  
¯¯¯¯  
              Arco  b = 1
          Angolo  α = 45°

Risultati:  
¯¯¯¯¯¯¯	 
          Raggio  r = 1.2732395
           Chord  s = 0.97449536
     Settore  A1 = 0.63661977
      Distanza  d = 1.17632
     Altitudine  h = 0,096919589
 Segmento  A2 = 0,063460604

            Area  A = 5.0929582
    Perimetro  p = 8

Tangenti dei cerchi   (nuovo nella versione 9.0 da febbraio 2021 )

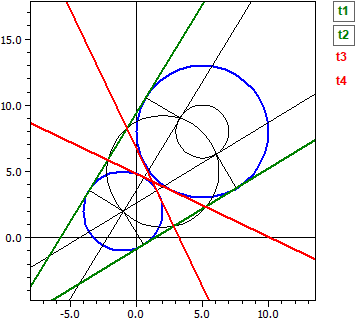
Vengono calcolate le equazioni delle seguenti tangenti a uno o due cerchi. Le costruzioni vengono disegnate e, se necessario, vengono visualizzate le linee di costruzione.

  • La tangente a un cerchio k in un punto B.
  • Le tangenti a un cerchio k attraverso un punto P esterno al cerchio
  • Le tangenti a un cerchio k parallelo a una retta g
  • Le tangenti a due cerchi ki e k2
Dato :
¯¯¯¯¯
  k1 : M(5|8) ,   r =5
  k2 : M(-1|2) ,   r =3

Tangenti esterne 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: -4,2923·x + 7,04104·y = -6,36427
  t2: -7,04104·x + 4,29230·y = 40,3643

Tangenti interne 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t3: 1,21895·x + 2,55228·y = 12,3709
  t4: -2,55228·x − 1,21895·y = -8,3709

Intersezioni nel piano

Il programma calcola le intersezioni di rette e cerchi.

Due rette

Dato :
¯¯¯¯¯
g : x + y = 0
h : x - y = 5

Punto di intersezione  S(2,5|-2,5)

Angolo di intersezione α = 90°

Distanze per l'origine
  d(g,O) = 0
  d(h,O) = 3,5355339

Cerchio e retta

Dato :
¯¯¯¯¯
  k : M(5|0)   r = 5
  g : x + y = 0

Punti di intersezione :      
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  S1(5|-5)
  S2(0|0)

Due cerchi

Dato :
¯¯¯¯¯
k1 : M1(5|5) r1 = 5
k2 : M2(0|0) r2 = 5

Punti di intersezione :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 
S1(5|0)   S2(0|5)

Retta di collegamento :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯   
 x + y = 5