MatheAss 10.0 − Analisi
Successiones e Series (Nuovo nella versione 9.0 da maggio 2021)
Il programma determina i primi n termini di una successione (ai) e la serie associata (somma dei termini della successione) se i primi termini della successione e una funzione esplicita ai=ƒ(i) o una formula di ricorso ai=ƒ(a0, a1, ... , ai-1) sono dati.
Successione ¯¯¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
Divisione dei polinomi
Il prodotto ed il quoziente di polinomi dovuti saranno calcolati.
1° polinomio: 3·x4 - 2 x + 1
2° polinomio: 2·x + 5
Prodotto: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Quoziente: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Resto: 1971/16
Fattorizzazione di polinomi (Nuovo nella versione 9.0)
Gli zeri razionali e la decomposizione di un polinomio in fattore lineare sono determinati.
p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
= (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
= (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)
Zeri rationali: 1/3, -1/3, 9, 3, -3
Trasformazione di polinomi (Nuovo nella versione 9.0)
Un polinomio p(x) può essere spostato o allungato nella direzione x e nella direzione y.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Spostato di dx = -2, dy = 0 ƒ(x + 2) = - 1/4 ·x4 + 6 ·x2 + 1
MCD e MCM di polinomi (Nuovo nella versione 9.0 da febbraio 2021)
Vengono determinati il massimo comune divisore (MCD) e il minimo comune multiplo (LCM) di due polinomi. p1(x) e p2(x).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 MCD(p1,p2) = x2 - x - 2 LCM(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
 Tracciatore di funzioni
Tracciatore di funzioni
È possibile tracciare fino a dieci funzioni contemporaneamente in un sistema di assi. è inoltre possibile utilizzare combinazioni o derivazioni di funzioni precedentemente definite.
Se f1(x)=sin(x) e f2(x)=3*sqrt(x), allora f3(x) = 2*y1^2-y2 sostituisce f3(x) = 2*sin(x)^2 - 3*sqrt(x) f4(x) = f2(y1) sostituisce f4(x) = 3*sqrt(sin(x)) f5(x) = y2' sostituisce f5(x) = 3/(2*sqrt(x))
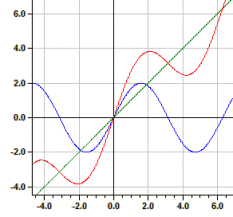
Esempio: ƒ1(x) = sin(x) ; ƒ2(x) = x ; ƒ3(x) = y1+y2
 Funzioni a tratti
Funzioni a tratti
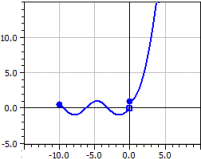
Viene disegnata una funzione definita da varie sottofunzioni, ciascuna definita su un certo sottodominio.
Esempio:
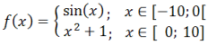
 Curve parametriche
Curve parametriche
Con questo programma si possono disegnare curve che non sono date da un termine di funzione esplicito, ma da due funzioni di deflessione orizzontale e verticale.
Esempio: Figura di Lissajous
x(k) = sin(3*k)
y(k) = cos(5*k)
k from -Pi to Pi
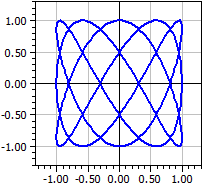
Le figure di Lissajou si ottengono quando due tensioni c.a. con frequenze diverse vengono applicate a un oscilloscopio.
 Famiglia di curve
Famiglia di curve
Il programma disegna i grafici di una funzione che contenga un parametro k. I valori per k possono essere elencati o determinati dal valore iniziale, dal valore finale e dal passo.
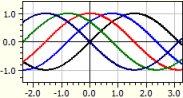
ƒ(x,k) = sin(x+k)
k da -2 a 2 con passo Pi/4
 Studio di funzioni polinomiali
(Nuovo nella versione 9.0)
Studio di funzioni polinomiali
(Nuovo nella versione 9.0)
Il programma svolge la discussione sulla curva per una funzione polinomiale. Ciò significa che
vengono determinati i derivati e la antiderivata
e la funzione viene esaminata per zeri razionali, per estremi, per punti di flesso e per simmetria.
Funzione:
¯¯¯¯¯¯¯¯
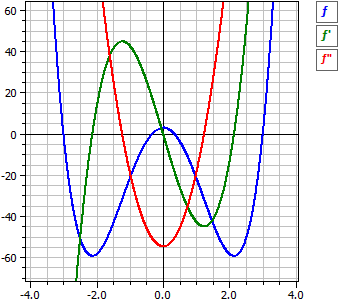
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Derivati:
¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Antiderivativa:
¯¯¯¯¯¯¯¯¯¯¯
F(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
 Studio di funzioni razionali
(Nuovo nella versione 9.0)
Studio di funzioni razionali
(Nuovo nella versione 9.0)
Il programma svolge la discussione sulla curva per una funzione razionale. Ciò significa che vengono determinate le derivati, le lacune nella definizione e la continuazione continua. La funzione viene esaminata per zeri, estremi, punti di flesso e comportamento di |x|→ ∞.
Funzione :
¯¯¯¯¯¯¯¯
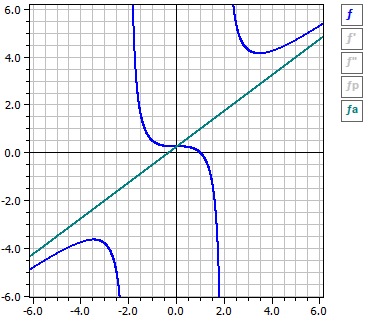
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Singularitás:
¯¯¯¯¯¯¯¯¯¯¯
x = 2 Palo con cambio di segno
x =-2 Palo con cambio di segno
Derivati:
¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = ————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ———————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
 Studio di funzioni arbitrarie
Studio di funzioni arbitrarie
Funzione: ‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4-2*x^3+1 Studio nella gamma da -10 to 10 Derivati: ‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Zeri: ‾‾‾‾‾‾‾ N1(1|0) m = - 2 N2(1,83929|0) m = + 4,5912 Estremi: ‾‾‾‾‾‾‾‾‾‾‾ T1(1,5|-0,6875) m = 0 Punti di flesso: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1(0|1) m = + 0 W2(1|0) m = - 2
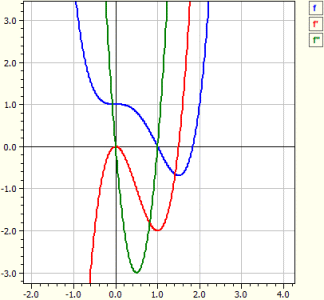
 Iterazione di Newton
Iterazione di Newton
Approssimazione degli zeri di una funzione ƒ(x) con il metodo del Newton con una prima congettura x0.
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
 Integral Calculus (from February 2021 with arc lengths)
Integral Calculus (from February 2021 with arc lengths)
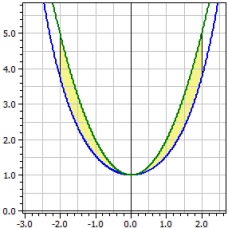
The oriented and absolute contents of the surface between two function curves are calculated at a desired interval [a; b].
In addition the twisting moments for rotation, the bodies of revolution and the arc lengths in the interval.
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Limits of integration from -2 to 2 Oriented content : A1 = -2,07961 Absolute content : A2 = 2,07961 Arc lengths : L1[a;b] = 7,254 L2[a,b] = 9,294
 Espansione in serie
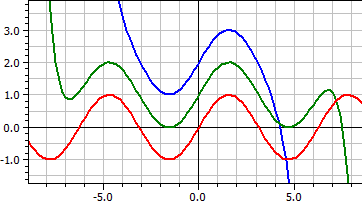
Espansione in serie
Tracciatore per le funzioni date come serie sopra la ƒ(x,k). Potete sviluppare la funzione con differenti gamme di parametro e differente y-sfalsi.
I primi 16 membri della serie Taylor per la funzione seno. ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 e 16
 Funzioni di superficie
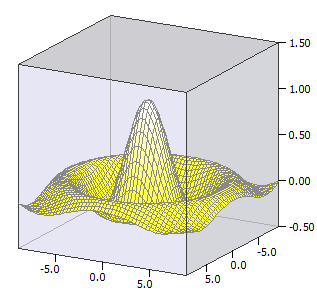
Funzioni di superficie
Tracciatore per una funzione di superficie ƒ(x,y), che può contenere un subterm u(x,y).
Esempio:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5