MatheAss 10.0 − Géométrie 3D
Systèmes de coordonnées
Conversion des coordonées cartésiennes en coordonnées polaires ou coordonnées cylindriques et vice versa.
cartésiennes polaires cylindriques x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Solides de Platon
Si une des grandeurs d'un tétraèdre, d'un hexaèdre, d'un octaèdre, d'un dodékaèdre ou d'un icosaèdre est donnée, le programme calcule les autres.
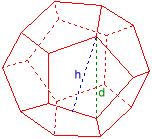
Exemple: Dodékaèdre
Entrées:
¯¯¯¯¯¯¯
Diag. de la face d = 2
Résultats:
¯¯¯¯¯¯¯¯
Arête a = 1,236068
Haut. de la face h = 1,902113
Sphère circonsc. rc = 1,7320508
Sphère inscrite r i = 1,3763819
Volume V = 14,472136
Surface S = 31,543867
Autres solides
Si deux des grandeurs d'un prisme régulier, d'un cylindre circulaire droit, d'une pyramide regulière, d'un cône circulaire droit ou d'une sphèresont données, le programme calcule les autres.
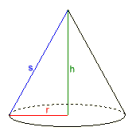
Exemple: Cône circulaire
Entrées:
¯¯¯¯¯¯¯
Volume V = 1
Base B = 1
Résultats:
¯¯¯¯¯¯¯¯
Rayon r = 0,56418958
Hauteur h = 3
Apothème s = 3,0525907
Surface latérale L = 5,4105761
Surface S = 6,4105761
Droite à travers 2 points
Droite à travers
A(1|1|1), B(2|5|6)
L'équation vectoriel
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Distance de l'origine
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Position au plan xy
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Projection: -4·x + y = 3
Intersec..: S1(0,8|0,2|0)
Angle : 50,490288°
Position au plan yz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Projection: -5·x + 4·y = 1
Intersec. : S2(0|-3|-4)
Angle : 8,8763951°
Position au plan xz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Projection: -5·x + y = 4
Intersec. : S3(0,75|0|-0,25)
Angle : 38,112927°
Plan à travers 3 points
Plan à travers
A(1|2|3), B(2|3|3),
C(1|0|1)
L'équation vectoriel:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
L'équ. en coordonées:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Distance de l'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Points de trace:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Sphère à travers 4 points
Sphère à travers: A(1|0|0), B(0|2|0), C(0|0|3), D(1|0|1) Forme normale: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ -> ⎧-2,5 ⎫ ⎫2 K:⎪ x - ⎪-0,5 ⎪ ⎪ = 12,75 ⎩ ⎩ 0,5 ⎭ ⎭ Le centre et le rayon: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ M(-2,5|-0,5|0,5) r = 3,570714
Intersections dans l'espace
Le programme détermine l'interséction entre deux droites, entre un plan et une droite, entre deux plans, entre une sphère et une droite, entre une sphère et un plan et entre deux sphères.
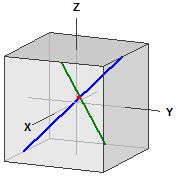
deux droites
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Point d'inters. : S(5|5|5)
Angle : α = 60°
Distances d'origine :
d(O,g)=5 d(O,h)=5
plan et droite
Le plan E :
¯¯¯¯¯¯¯¯¯¯¯¯
E : x + y + z = 5
La droite g :
¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Le point d'intersection :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S(5|0|0)
L'angle d'intersection :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
alpha = 54,73561°
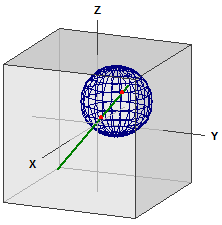
sphère et droite
La sphère :
¯¯¯¯¯¯¯¯¯¯¯
K : M(5|5|5) , r = 5
La droite :
¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Points d'intersection :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S1(2,81867|1,81867|1,81867)
S2(8,51467|7,51467|7,51467)
Longueur de la corde :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
s = 9,8657657
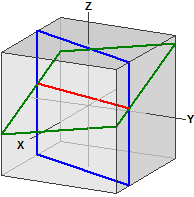
deux plans
Les deux plans:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 :·x - y + 5·z = 8
La droite d'intersection:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧-11 ⎫ ⎧ 10 ⎫
g : x = ⎪-30 ⎪ + r·⎪ 25 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
La distance de l'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
L'angle entre les plans:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
alpha = 65,993637°
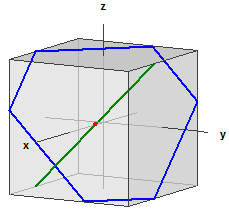
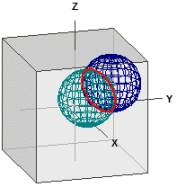
deux sphères
Les deux sphères: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Le cercle d'intersection: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2) , r = 2,4494897 Le plan d'intersection: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
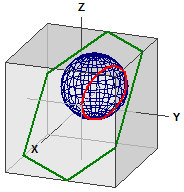
sphère et plan
Le plan:
¯¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
La Sphère:
¯¯¯¯¯¯¯¯¯¯
⎧ -> ⎧ 1 ⎫⎫2
K : ⎪ x - ⎪ 2 ⎪⎪ = 16
⎩ ⎩ 3 ⎭⎭
Le cercle d'intersection:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,14|2,91|1,86)
r = 3,55
Distances sur la sphère
(Nouveau en version 9.0 depuis décembre 2021)
La distance entre deux points sur une sphère est calculée.
GPS decimal ¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS dms ¯¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Distance ¯¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112
