MatheAss 9.0 − Géométrie 2D

Triangles rectangles

Si deux grandeurs d'un triangle rectangle sont données le programme calcule les autres.

Entrées:
¯¯¯¯¯¯¯	  
    a = 3   et   c = 5
 
Résultats :
¯¯¯¯¯¯¯¯
                    Cathète b = 4
                       Angle α = 36,869898°
                       Angle β = 53,130102°
                    Hauteur h = 2,4
Part de l'hypoténuse p = 1,8
Part de l'hypoténuse q = 3,2
                          Aire A = 6

Triangles par 3 grandeurs

Des triangles sont déterminés par trois grandeurs extérieur (côtés ou angles) si l'une des congruences suivantes sont remplies:

sss trois côtés sont données.
sww un côté et deux angles sont donnés.
sws deux côtés et l'angle fermé sont données
Ssw deux côtés et l'angle opposé de la grande côté sont donnés.

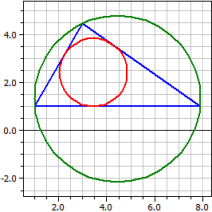
Entrées: a=6, b=4 et α=60°

 Sommets:   A(1|1)         B(7,899|1)   C(3|4,4641)
       Côtés:   6                4                  6,89898
     Angles:   60°             35,2644°     84,7356° 
 Hauteurs:   3,98313      5,97469      3,4641 
  Médians:   4,77472      6,148          3,75513
  Bisséctr.:   4,38551      6,11664      3,5464

C.circon.:   M(4,44949|1,31784)       ru = 3,4641
C.inscrit :   O(3,44949|2,41421)        ri = 1,41421

       Aire:   A = 11,9494     Périmetre u = 16,899

Triangles par 3 points

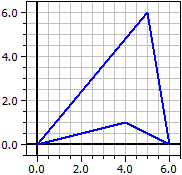
Si les coordonnées des trois points d'un triangle sont données, le programme calcule les côtés, les angles, les hauteurs, les médianes, les bisséctrices, la circonférence et l'aire.

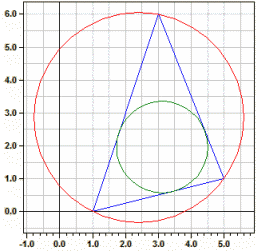
 Sommets :  A(1|0)            B(5|1)            C(3|6)
       Côtés : 5,38516         6,32456         4,12311
      Angles : 57,5288°       82,2348°       40,2364°
  Hauteurs : 4,0853          3,47851         5,33578
   Médians : 4,60977        3,60555        5,5
   Bisséctr. : 4,37592        3,51849        5,46225

 C.circon. : M(2,40909|2,86364)       ru = 3,19154
 C.inscrit  : O(3,11866|1,96195)       ri = 1,38952

       Aire : A = 11        Périmètre : u = 15,8328

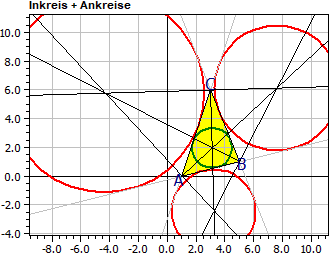
Lignes spéciales dans un triangle (Nouveau en version 9.0)

Le programme calcule les équations des médiatrices, des medianes, des bissectrices et des altitudes d'un triangle. De plus, les centres et les rayons du cercle circonscrit, du cercle inscrit et des trois cercles exinscrits.

Entrées:
¯¯¯¯¯¯¯
   Sommets:  A(1|0)   B(5|1)   C(3|6)
 
Résultats: 
¯¯¯¯¯¯¯¯
                 Côtés: a :  5·x + 2·y = 27
                            b :  3·x - y = 3
                            c :  x - 4·y = 1
 
     Cercle inscrit: Mi(3,119|1,962)         r i = 1,390
 
Cercles exinscr.: Ma(7,626|6,136)       ra = 4,346
                           Mb(-4,356|5,784)      rb = 6,910
                           Mc(3,248|-2,427)      rc = 2,900

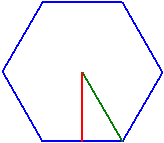
Polygones réguliers

Si une des grandeurs suivantes d'un polygone régulier avec n sommets est donnée, le programme calcule les autres:
La côte, le rayon du cercle circonférent, le rayon du cercle inscrit, le périmètre ou l'aire.

Entrées:
¯¯¯¯¯¯¯
        Sommets  n = 6
 Cercle circon. rc = 1
 
Resultats:  
¯¯¯¯¯¯¯¯ 
             Côté  a = 1
 Cercle inscrit ri = 0,8660254
     Périmètre  p = 6
               Aire A = 2,5980762

Polygones arbitraires

L'aire, la circonférence et les centres d'un polygone sont calculés.

Points:      Aire  A = 18
 A(0|0)     
 B(4|1)     Circonférence  p = 22,032567
 C(6|0)     
 D(5|7)     Centre de gravités de points:
                CP(3,75|2)
            
                Centre de gravités de l'aire:
                CA(3,72222|2,66667)

Applications d'un Polygone (Révisé en version 9.0)

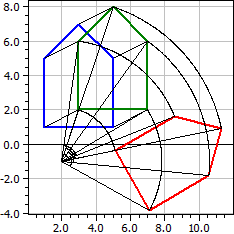
Les applications possibles sont: le déplacement parallèle, la symétrie axiale, la symétrie ponctuelle, la rotation, l'allongement et la cisaillement.

Polygone originale
A(1|1), B(5|1), C(5|5), D(3|7), E(1|5), 

1. Déplacement parallèle: dx=2, dy=1  ☑ 

2. Rotation: Z(2|-1), α=-60°  ☑
A(5,0981|-0,36603), B(7,0981|-3,8301), 
C(10,562|-1,8301), D(11,294|0,90192),
E(8,5622|1,634)

Cercles et ses parts

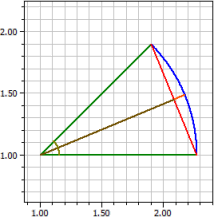
Si deux des grandeurs suivantes d'une section circulaire sont données, le programme calcule les autres :
Le rayon, l'angle;, l'arc, la corde, la section, le segment, l'aire, le périmètre, la distane de la corde et l'altitude de l'arc.

Entrées:
¯¯¯¯¯¯¯  
             Arc b = 1
         Angle α = 45°

Resultats:  
¯¯¯¯¯¯¯¯  
        Rayon r = 1,2732395
        Corde s = 0,97449536
   Section A1 = 0,63661977
   Distance d = 1,17632
     Altitude h = 0,096919589
Segment A2 = 0,063460604

          Aire A = 5,0929582
Périmètre p = 8

Tangentes aux cercles (Nouveau en version 9.0 depuis février 2021)

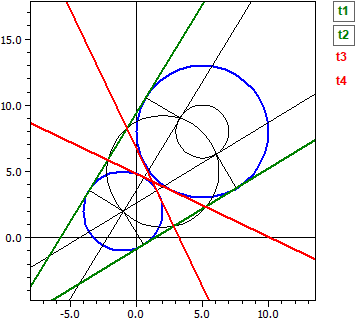
La tangente à un cercle k en un point B.
Les tangentes à un cercle k passant par un point P en dehors du cercle
Les tangentes à un cercle k parallèle à une droite g
Les tangentes à deux cercles k₁ et k₂

Entrées:
¯¯¯¯¯¯¯
 k₁ : M(5|8) ,   r =5
 k₂ : M(-1|2) ,   r =3

Tangentes extérieures
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 t₁: -4,2923·x + 7,04104·y = -6,36427
 t₂: -7,04104·x + 4,29230·y = 40,3643

Tangentes intérieures
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 t₃: 1,21895·x + 2,55228·y = 12,3709
 t₄: -2,55228·x − 1,21895·y = -8,3709

Intersections dans le plan

Le programme détermine l'intersection de deux droites, d'un cercle et d'une droite et de deux cercles.

deux droites

g : x + y = 0
h : x − y = 5

Point d'intersection : 
  S(2,5|-2,5)

Angle entre g et h : 
 α = 90°

Distances d'origine  :
  d(g,O) = 0
  d(h,O) = 3,5355339

cercle et droite

Le cercle et la droite :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  k : M(5|0)   r = 5
  g : x + y = 0

Points d'intersection :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  S₁(5|-5)  S₂(0|0)

deux cercles

Les deux cercles :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  k₁ : M₁(5|5)   r₁ = 5
  k₂ : M₂(0|0)   r₂ = 5

Points d'intersection :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  S₁(5|0)  S₂(0|5)

Droite de jonction :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  x + y = 5

fra.matheass.eu