MatheAss 10.0 − Stochastique
Statistiques
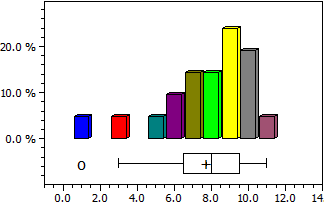
Ce module calcule la moyenne, la médiane, la variance et l'écart-type d'une série d'observations, et génère un histogramme.
Données :
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Nombre de données n = 21
Maximum max = 11
Minimum min = 1
Moyenne x = 7,7142857
Médiane c = 8
Variance s2 = 6,1142857
Écart-type s = 2,4727082
Régression
Ce module ajuste une série de points selon les types de régression suivants :
- Régression proportionnelle y = b·x
- Régression linéaire y = a + b·x
- Régression polynomiale y = a0 + ... + an·xn
- Régression géométrique y = a·xb
- Régression exponentielle y = a·bx
- Régression logarithmique y = a + b·ln(x)
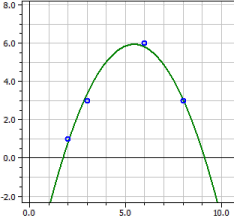
Régression polynomiale
y = −6,9152542
+ 4,7189266·x
− 0,43361582·x2
Coeff. de détermination = 0,98338318
Coeff. de corrélation = 0,99165679
Écart-type = 0,46028731
Régression logistique (Nouveau en version 9.0)
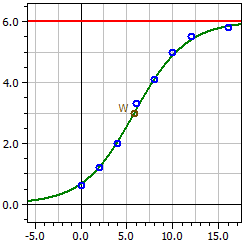
Ce module ajuste une série de mesures à une courbe logistique
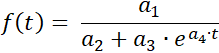
avec les paramètres a1 = ƒ(0)·S, a2 = ƒ(0), a3 = S − ƒ(0),
et a4 = −k·S, où S est la limite de saturation.
Données : "hopfenwachstum.csv"
Limite de saturation : 6
Figure sombre : 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Point d'inflexion W(5,8226 / 3)
Taux de croissance maximal ƒ'(xw) = 0,53433
8 valeurs
Coeff. de détermination = 0,99383916
Coeff. de corrélation = 0,99691482
Écart-type = 0,16172584
Combinatoire
Ce module calcule le nombre de sélections de k éléments parmi un ensemble de n. Il distingue les arrangements et les combinaisons, avec ou sans répétition, ainsi que les permutations.
n = 49, k = 6 Arrangements sans répétition n! / (n−k)! = 10 068 347 520 Arrangements avec répétition n^k = 13 841 287 201 Combinaisons sans répétition n sur k = 13 983 816 Combinaisons avec répétition n+k−1 sur k = 25 827 165 Permutations de k éléments k! = 720
Distribution binomiale
Pour une variable aléatoire X suivant la loi b(k;n;p) avec n et p donnés, le module calcule :
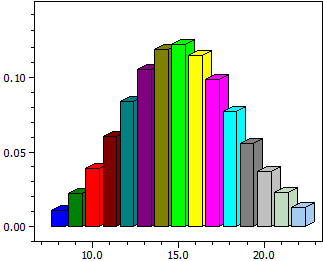
- un histogramme des probabilités P(X = k)
- les valeurs numériques dans un intervalle [kmin; kmax]
- la probabilité P(kmin ≤ X ≤ kmax)
n = 50 p = 0,3
k P(X=k) P(0<=X<=k)
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
8 0,01098914 0,01825335
9 0,02197829 0,04023163
10 0,03861899 0,07885062
11 0,06018544 0,13903606
12 0,08382972 0,22286578
13 0,10501745 0,32788324
14 0,11894834 0,44683157
15 0,12234686 0,56917844
16 0,11470018 0,68387862
17 0,09831444 0,78219306
18 0,07724706 0,85944012
19 0,05575728 0,91519740
20 0,03703876 0,95223616
21 0,02267679 0,97491296
22 0,01281092 0,98772387
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
P(8<=k<=22) = 0,98045967
Distribution hypergéométrique
Pour une variable aléatoire X distribué de h(k;n;m;r) avec n,m et r donnés, le programme calcul un histogramme des probabilitées P(X=k), leurs valeurs numériques dans un intervalle [kmin;kmax], et la probabilité P( kmin≤X≤kmax).
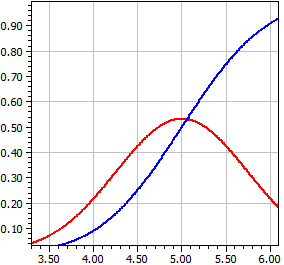
Distribution normale
Pour une variable aléatoire distribuée N(µ, σ2), avec l'estimation μ et la variante σ2, le programme trace la fonction de densité ƒ(x) et la fonction de distribution Φ(x), c'est-à-dire l'intégrale sur ƒ(x).
μ = 5 , σ = 0.75
x ƒ(x) Φ(x)
¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
2 0,00017844 0,00003167
2,33333333 0,00095649 0,00018859
2,66666666 0,00420802 0,00093192
2,99999999 0,01519465 0,00383038
3,33333332 0,04503153 0,01313415
3,66666665 0,10953585 0,03772017
3,99999998 0,21868009 0,09121120
4,33333331 0,35832381 0,18703139
4,66666664 0,48189843 0,32836063
4,99999997 0,53192304 0,49999998
5,33333333 0,48189845 0,67163934
5,66666663 0,35832383 0,81296859
5,99999996 0,21868012 0,90878878
6,33333329 0,10953586 0,96227982
6,66666662 0,04503154 0,98686585
6,99999995 0,01519465 0,99616962
7,33333328 0,00420802 0,99906808
7,66666661 0,00095649 0,99981141
7,99999994 0,00017844 0,99996833
