MatheAss 10.0 − Analyse
Suites et Séries (Nouveau en version 9.0 depuis mai 2021)
Le logiciel détermine les n premiers termes d'une suite (ai) et la série associée (somme des termes de la suite) si les premiers termes de la suite et une fonction explicite ai=ƒ(i) ou une formule de recours ai=ƒ(a0, a1, ... , ai-1) sont donnés.
Suite ¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Série ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
Divison des plolynômes
Le programme calcule le produit et le quotient des deux polynômes.
1. Polynôme: 3x4 - 2x + 1
2. Polynôme: 2x + 5
Produit: 6x5 + 15x4 - 4x2 - 8x + 5
Quotient: 3/2x3 - 15/4x2 + 75/8x - 391/16
Résidu: 1971/16
Factoriser des polynômes (Nouveau en version 9.0)
Les zéros rationnels et la décomposition d'un polynôme en facteurs linéaires sont déterminés.
p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
= (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
= (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)
Zéros rationnels : 1/3, -1/3, 9, 3, -3
Transformer les polynômes (Nouveau en version 9.0)
Un polynôme p(x) peut être déplacé ou étiré dans la direction x et la direction y.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Déplacé par dx = -2, dy = 0 ƒ(x + 2) = - 1/4 ·x4 + 6 ·x2 + 1
Polynômes PGCD et PPCM (Nouveau en version 9.0 depuis février 2021)
Le plus grand commun diviseur(PGCD) et le plus petit commun multiple (PPCM) de deux polynômes sont déterminés.
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 PGCD(p1,p2) = x2 - x - 2 PPCM(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
Traceur des fonctions
Un traceurs pour plusieurs fonctions dans un même système de coordonnée. Des concaténation ou des dérivés de fonctions déjà définies sont également possibles.
Si ƒ1(x) = sin(x) et ƒ2(x) = 3*sqrt(x), alors ƒ3(x) = 2*y1^2-y2 remplace ƒ3(x) = 2*sin(x)^2-3*sqrt(x) ƒ4(x) = f2(y1) remplace ƒ4(x) = 3*sqrt(sin(x)) ƒ5(x) = y2' remplace ƒ5(x) = 3/(2*sqrt(x))
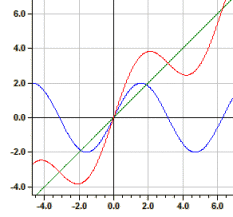
Exemple: ƒ1(x)=sin(x), ƒ2(x)=x and ƒ3(x)=y1+y2
Fonctions par morceaux
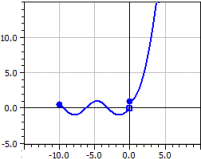
Une fonction définie sur une réunion d'intervalles par jusqu'à neuf sous-fonctions est tracée. Pour chacune des sous-fonctions, la zone de définition, le type d'intervalle et la couleur sont renseignés.
Exemple:
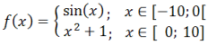
Courbes paramétriques
Une courbe donnée par une représentation avec paramêtres est tracée.
Les courbes de Lissajou
x(k) = sin(3*k)
y(k) = cos(5*k)
k de -Pi à Pi
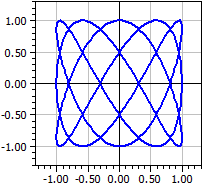
Des figures de Lissajou sont obtenus lorsque deux tensions alternatives de fréquences différentes sont appliquées à un oscilloscope.
Famille de courbes
Le programme trace des fonctions qui contient un paramètre de lame k. Les valeurs de k peuvent être répertoriées ou déterminées par valeur initiale, valeur finale et taille de pas.
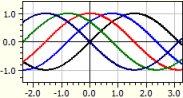
ƒ(x,k) = sin(x+k)
k de -2 à 2 avec pas Pi/4
Études des fonctions polynomiales (Nouveau en version 9.0)
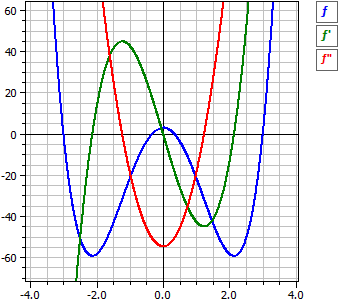
Le programme exécute la discussion de la courbe pour une fonction polynomiale. Cela signifie que les dérivées et l'antidérivatif sont déterminées. La fonction est examinée pour les zéros rationnels, pour les extrêmes, pour les points de retournement et pour la symétrie.
Fonction:
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Dérivées:
¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Antidérivatif:
¯¯¯¯¯¯¯¯¯¯¯
F(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
Études des fonctions rationnelles (Nouveau en version 9.0)
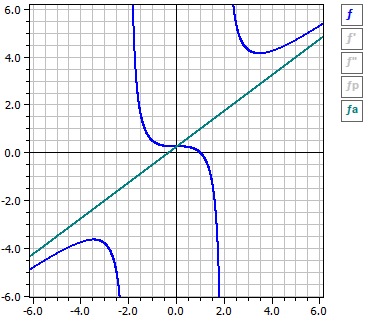
Le programme exécute la discussion de courbe pour une fonction rationnelle (brisée). Cela signifie que les dérivées et la domaine de définition sont déterminées. La fonction est examinée pour les zéros, les extrêmes, les points d'inflexion et le comportement pour |x|→ ∞.
Fonction :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Lacunes de définition:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2 Pôle avec changement de signe
x =-2 Pôle avec changement de signe
Dérivées:
¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = ————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ———————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
Études des fonctions arbitraires
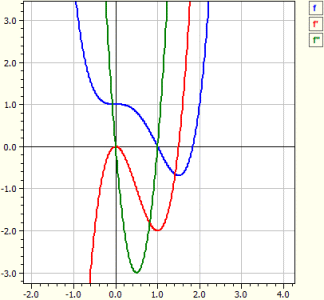
Le programme effectue la discussion de la courbe pour n'importe quelle fonction. Les dérivées sont déterminées, la fonction est examinée pour les zéros, les extrema et les points de retournement, les graphiques de ƒ, ƒ' et ƒ" sont tracées et un tableau de valeurs est généré.
Function: ‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4-2*x^3+1 Domaine de l'étude de -10 à 10 Dérivées: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Zéros: ‾‾‾‾‾‾‾‾ N1(1|0) m = - 2 N2(1,83929|0) m = + 4,5912 Extrema: ‾‾‾‾‾‾‾‾‾‾‾‾‾ T1(1,5|-0,6875) m = 0 Pts d'inversions: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1(0|1) m = + 0 W2(1|0) m = - 2
Itération de Newton
Approximation des valeurs nulles d'une fonction d'après la méthode de Newton avec une valeur initiale x0.
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Calcule integral (depuis février 2021 avec des longueurs d'arc)
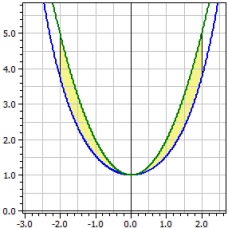
Les contenus orientés et absolus de la surface entre deux courbes de fonction dans un intervalle [a ; b] sont calculés.
Outre les moments de torsion pour la rotation, les corps de révolution et les longueurs d'arc dans l'intervalle.
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Intervall [a, b] de -2 à 2 Surcace orientée : A1 = -2,07961 Surface absolu : A2 = 2,07961 Longueurs d'arc : L1[a;b] = 7,254 L2[a,b] = 9,294
Développement en série
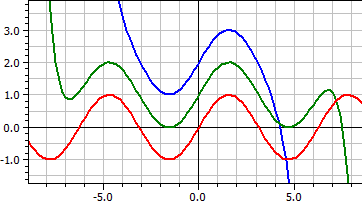
Une fonction donnée par une série de ƒ(x,k) est tracée. Plusieurs développements en série peuvent être comparés et déplacés en direction de y pour une meilleure distinction.
Les 16 premiers membres de la série Taylor pour la fonction sinus. . ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 et 16
Fonctions de l'aire
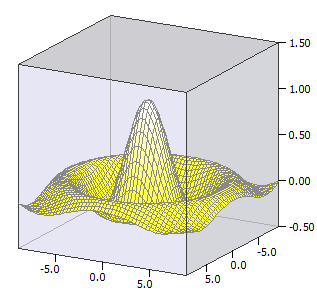
Une fonction de l'aire ƒ(x,y) est tracée. Cela veut dire une surface defini par une fonction avec deux variables.
Exemple:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5
