MatheAss - Olasılık

İstatistik

Bir ana liste için, ortalama (aritmetik ortalama), merkezi değer (medyan), varyans ve standart sapma belirlenir. Ayrıca, dağılım bir histogram ve kutu grafiği olarak gösterilir.

Regresyon

Bu rutin ile bir dizi ölçüm için bir eğri uyumu yapabilirsiniz. Aşağıdaki ayarlamalar arasından seçim yapabilir ve gerekirse tüm noktaları x veya y yönünde taşıyabilir veya genişletebilirsiniz.

Orantısal regresyon ( y = a·x )

Doğrusal regresyon ( y = a·x + b )

n'inci dereceden polinom regresyonu ( y = a₀ + ... + a_n·xⁿ )

Geometrik regresyon ( y = a·x^b )

Üstel regresyon ( y = a·b^x )

Logaritmik regresyon ( y = a + b·ln(x) )

Lojistik Regresyon

Program, bir dizi ölçüm için lojistik fonksiyona bir eğri uyumu belirler

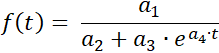
şu parametrelerle a₁ = ƒ(0)· S , a₂ = ƒ(0) , a₃ = S - ƒ(0) , ve a₄ = -k· S ve doyum sınırı S .

Kombinatorik

n elemandan k'nın seçilme olasılık sayısı, sıralama değerli olup olmadığı ve tekrarlara izin verilip verilmediği durumlarda hesaplanır.

Binom Dağılımı

b(k;n;p) dağılımlı bir rastgele miktar X için, sabit n ve sabit p değerlerinde hesaplanır:

- Olasılıkların P(X=k) çubuk grafiği
- [k-min;k-max] aralığındaki sayısal değerleri
- P( k-min < = X <= k-max) olasılığı

Hipergeometrik Dağılım

Sabit n, m ve sabit r değerlerinde, h (k; n; m; r) dağılımlı bir rastgele değişken X için olasılık P(X=k) çubuk grafiği ve değer tablosu hesaplanır.

Normal Dağılım

N(µ, σ²) dağılımlı bir rastgele değişken X için, verilen beklenen değer µ ve varyans σ² ile yoğunluk fonksiyonu ƒ(x) ve dağılım fonksiyonu Φ(x), yani ƒ(x) üzerinde integral hesaplaması yapılır.