MatheAss 10.0 − Geometría 3D
Sistemas de coordenadas
Con este programa, las coordenadas cartesianas tridimensionales se pueden convertir en coordenadas polares o coordenadas cilíndricas y viceversa.

cartesiano polares cilíndrico x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
 Sólidos platónicos
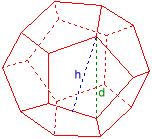
Sólidos platónicos
El programa calcula los cinco sólidos platónicos tetraedro, hexaedro, octaedro, dodecaedro e icosaedro si se dan la longitud del borde, la altura del Área, la altura de la habitación, el radio de la esfera interior, el radio de la esfera exterior, el volumen o la superficie.
Ejemplo: Dodecaedro
Dado:
¯¯¯¯¯
Diagonal de la cara d = 2
Resultados:
¯¯¯¯¯¯¯¯¯
Borde a = 1,236068
Altura de la cara h = 1,902113
Esfera circunscr. rc = 1,7320508
Esfera inscrita ri = 1,3763819
Volumen V = 14,472136
Superficie S = 31,543867
 Otros sólidos
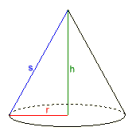
Otros sólidos
El programa calcula todas las cantidades de un prisma regular, un cilindro circular vertical, una pirÁmide regular, un cono circular recto o una esfera dados dos de ellos.
Ejemplo: Cono circular recto
Dado:
¯¯¯¯¯
Volumen V = 1
Base B = 1
Resultados:
¯¯¯¯¯¯¯¯¯
Radio r = 0,56418958
Altura h = 1
Perímetro p = 3,5449077
Superficie lateral L = 3,5449077
Superficie S = 5,5449077
Recta a través de 2 puntos
Recta a través de
A(1|1|1), B(2|5|6)
Representación paramétrica
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Distancia desde el origen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Posición con respecto al plano xy
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.Proj: 4·x - y = 3
Schnittpkt: S1(0,8|0,2|0)
Schnittwkl: 50,490288°
Posición con respecto al plano yz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.Proj: 5·x - 4·y = 1
Schnittpkt: S2(0|-3|-4)
Schnittwkl: 8,8763951°
Posición con respecto al plano xz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.Proj: 5·x - y = 4
Schnittpkt: S3(0,75|0|-0,25)
Schnittwkl: 38,112927°
Plano través de 3 puntos
Plano través de los puntos:
A(1|2|3), B(2|3|3), C(1|0|1)
Forma punto-pendiente:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Ecuación en coordenadas:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Distancia desde el origen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Puntos de seguimiento:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Esfera a través de 4 puntos
Esfera a través de:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Forma normal:
¯¯¯¯¯¯¯¯¯¯¯¯¯
| -> ⎧-2,5 ⎫ |2
K: | x - ⎪-0,5 ⎪ | = 12,75
| ⎩ 0,5 ⎭ |
Centro y radio:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
 Intersecciones en el espacio
Intersecciones en el espacio
Las intersecciones entre dos líneas, una línea y el plano, dos planos, una línea y una esfera, un plano y una esfera y entre las dos esferas se calculan.
Dos rectas
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Punto de intersección:
S(5|5|5)
Ángulo de intersección:
α = 60°
Distancias de origen :
d(O,g)=5 d(O,h)=5
Plano y recta
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
E : x + y + z = 5
Punto de intersección:
S(5|0|0)
Ángulo de intersección:
α = 54,73561°
Esfera y recta
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
K : M(5|5|5) , r = 5
Puntos de intersección :
S1(2,8187|1,8187|1,8187)
S2(8,5147|7,5147|7,5147)
Longitud de la cuerda:
s = 9,8657657
Dos planos
Dado los planos:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
Recta de intersección:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> |-11 | | 10 |
g : x = |-30 | + r·| 25 |
| 0 | | 1 |
Distancia desde el origen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
Ángulo de intersección:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
Dos esferas
Dado las esferas: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Círculo de la intersección: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Plano de la intersección: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
Esfera y plano
Plano :
¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Esfera :
¯¯¯¯¯¯¯
| -> ⎧ 1 ⎫|2
K : | x - ⎪ 2 ⎪| = 16
| ⎩ 3 ⎭|
Círculo de la intersección:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,13636|2,9091|1,8636)
r = 3,548367
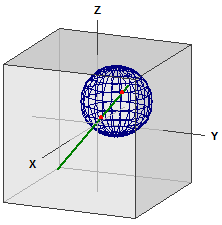
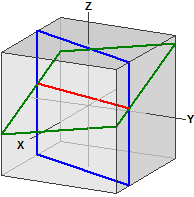
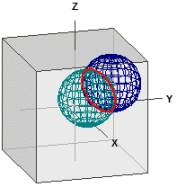
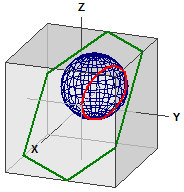
 Distancias en la esfera
(Nuevo en la versión 9.0 desde diciembre de 2021)
Distancias en la esfera
(Nuevo en la versión 9.0 desde diciembre de 2021)
Se calcula la distancia entre dos puntos en una esfera.
GPS decimal ¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS dms ¯¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Distancia ¯¯¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112

