MatheAss - Estocástica
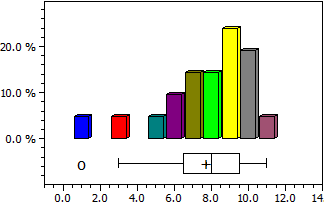
Estadísticas
La media, mediana, desviación estándar y varianza de una muestra y el histograma correspondiente se calculan. AdemÁs, la distribución se muestra como un histograma y como un diagrama de caja.
Datos:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Número de datos n = 21
MÁxima max = 11
Mínima min = 1
Media x = 7,7142857
Mediana c = 8
Varianza s² = 6,1142857
Desviación estándar s = 2,4727082
Regresión
La curva de regresión para adaptarse a una muestra de puntos se calcula. Son compatibles regresión proporcional, regresión lineal, regresión geométrica, regresión exponencial, regresión logarítmica y regresión polinomio
Regresión proporcional ( y = a·x )
Regresión lineal ( y = a·x + b )
Regresión polinómica de orden n ( y = a0 + ... + an·xn )
Regresión geométrica ( y = a·xb )
Regresión exponencial ( y = a·bx )
Regresión logarítmica ( y = a + b·ln(x) )
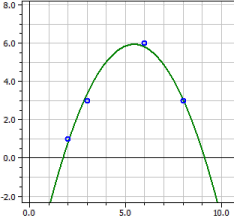
Regresión polinómica
y = - 6,9152542
+ 4,7189266·x
- 0,43361582·x2
4 Valores
Coeficiente de determinación = 0,98338318
Coeficiente de correlación = 0,99165679
Desviación estÁndar = 0,46028731
Regresión logística
(Nuevo en la versión 9.0)
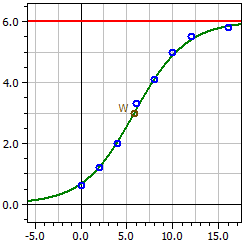
El programa determina para una serie de medidas una curva que se ajusta a la función logística
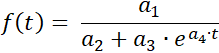
con los parámetros
a1 = ƒ(0)·S ,
a2 = ƒ(0) , a3 = S - ƒ(0) ,
a4 = -k·S y el límite de saturación S .
Datos de: "\Hopfenwachstum.csv"
Límite de saturación: 6
Figura oscura: 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Punto de inflexión W(5,8226/3)
Tasa de crecimiento mÁxima ƒ'(xw) = 0,53433
8 Valores
Coeficiente de determinación = 0,99383916
Coeficiente de correlación = 0,99691482
La desviación estÁndar = 0,16172584
Combinatoria
El número de variaciones y combinaciones de las k de n elementos, con o sin repeticiones se calculan.
n = 49 k = 6 Variaciónes sin repetitiones = 10 068 347 520 Variaciónes con repeticiones = 13 841 287 201 Combinaciones sin repetitiones = 13 983 816 Combinaciones con repeticiones = 25 827 165 Permutaciones de k : k! = 720
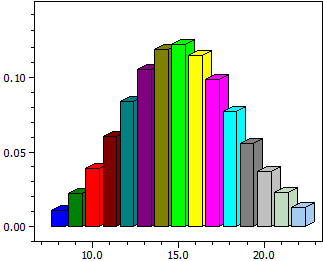
Distribución binomial
Por una variable aleatoria X distribuido b(k,n,p) con n fijo y p recibe
− un histograma de las probabilidades P(X=k)
− una tabla de sus valores de kmin a kmax
− la probabilidad P(kmin≤X≤kmax).
n = 50 p = 0,3
k P(X=k) P(0≤X<k)
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
8 0,01098914 0,01825335
9 0,02197829 0,04023163
10 0,03861899 0,07885062
11 0,06018544 0,13903606
12 0,08382972 0,22286578
13 0,10501745 0,32788324
14 0,11894834 0,44683157
15 0,12234686 0,56917844
16 0,11470018 0,68387862
17 0,09831444 0,78219306
18 0,07724706 0,85944012
19 0,05575728 0,91519740
20 0,03703876 0,95223616
21 0,02267679 0,97491296
22 0,01281092 0,98772387
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
P(8 ≤ k < 22) = 0,98045967
Distribución hipergeométrica
Por una variable aleatoria X distribuido b(k,n,m,r) con n fijo, m y r , recibe un histograma de las probabilidades P(X=k), una tabla de sus valores de kmin a kmax y la probabilidad P(kmin≤X≤kmax).
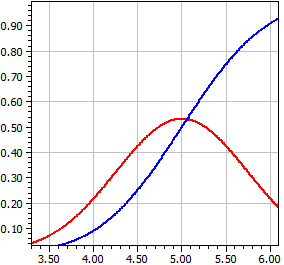
Distribución normal
Por una variable aleatoria X distribuido N(µ, σ2) con la media μ y la varianza σ2 recibe la función de densidad y la función de distribución.
μ = 5 , σ = .75
x ƒ(x) Φ(x)
¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
2 0,00017844 0,00003167
2,33333333 0,00095649 0,00018859
2,66666666 0,00420802 0,00093192
2,99999999 0,01519465 0,00383038
3,33333332 0,04503153 0,01313415
3,66666665 0,10953585 0,03772017
3,99999998 0,21868009 0,09121120
4,33333331 0,35832381 0,18703139
4,66666664 0,48189843 0,32836063
4,99999997 0,53192304 0,49999998
5,3333333 0,48189845 0,67163934
5,66666663 0,35832383 0,81296859
5,99999996 0,21868012 0,90878878
6,33333329 0,10953586 0,96227982
6,66666662 0,04503154 0,98686585
6,99999995 0,01519465 0,99616962
7,33333328 0,00420802 0,99906808
7,66666661 0,00095649 0,99981141
7,99999994 0,00017844 0,99996833
