MatheAss 10.0 − Análisis
Secuencias y series (Nuevo en la versión 9.0 desde mayo de 2021)
El programa determina los primeros n términos de una secuencia (ai) y la serie asociada (suma de los términos de la secuencia) se dan los primeros términos de la secuencia y una fórmula de recurso ai=ƒ(a0, a1, ... , ai-1) o una función explícita ai=ƒ(i).
a[0]=1; a[1]=1; a[ i ] = a[i-1] + a[i-2]; n = 20 Sucesión ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Serie ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
División de Polinomios
El producto y el cociente de dos polinomios será calculado.
1. Polinomio: 3·x4 - 2·x + 1
2. Polinomio: 2·x + 5
Producto: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Cociente: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Resto: 1971/16
Factorización de polinomios (Nuevo en la versión 9.0)
Se determinan los ceros racionales y la descomposición de un polinomio en factores lineales.
p(x) = x5 + 3x4 + 8/3x3 - x - 1/3 â€&Permil; = 1/3·(3x5 + 9x4 + 8x3 - 3x - 1) â€&Permil; = 1/3·(x + 1)3·(3x2 - 1) Zeros racionales : -1 Ceros irracionales: -0,57735, 0,57735
Transformación de polinomios (Nuevo en la versión 9.0)
Un polinomio p(x) può essere spostato o allungato nella direzione x e nella direzione y.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Desplazado por dx = -2 , dy = 0 ƒ(x + 2) = - 1/4·x4 + 6·x2 + 1
MCD y MCM de polinomios (Nuevo en la versión 9.0 desde febrero de 2021)
Se determinan el máximo común divisor (MCD) y el mínimo común múltiplo (mcm) de dos polinomios p1(x) y p2(x).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 MCD(p1,p2) = x2 - x - 2 mcm(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
Trazadores de funciones
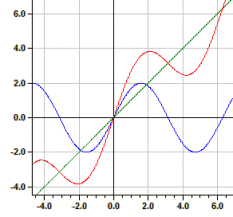
Se pueden trazar hasta diez funciones en un sistema de coordenadas a la vez. También puede utilizar combinaciones o derivaciones de funciones ya definidas.
Si ƒ1(x)=sin(x) y ƒ2(x)=3*sqrt(x) , entonces ƒ3(x)=2*y1^2-y2 sustituye a ƒ3(x)=2*sin(x)^2-3*sqrt(x) ƒ4(x)=f2(y1) sustituye a ƒ4(x)=3*sqrt(sin(x)) ƒ5(x)=y2' sustituye a ƒ5(x)=3/(2*sqrt(x))
Ejemplo: ƒ1(x)=sin(x), ƒ2(x)=x und ƒ3(x)=y1+y2
Funciones por partes
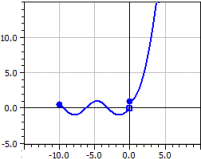
Se traza una función definida por partes, determinada por funciones parciales ƒ1 a ƒ9 .
El dominio de definición y el modo de intervalo y el color se ingresan para cada función parcial.
Ejemplo:
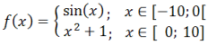
Curvas paramétricas
Las curvas, que no están determinadas por un término de función explícito, sino por dos funciones para la dirección horizontal y vertical, se pueden trazar con este programa.
Ejemplos:
1. El círculo x(k)=sin(k), y(k)=cos(k),
k de -π a π
2. La Espiral x(k)=k*sin(k), y(k)=k*cos(k),
k de 0 a 20
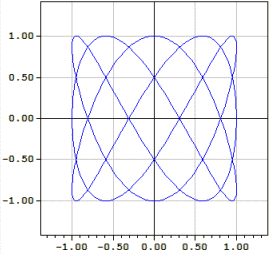
3. Las figuras de Lissajou:
x(k)=sin(3*k), y(k)=cos(5*k), k de -π a π
Familia de curvas
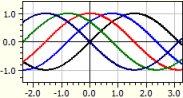
El programa traza diagramas de cualquier función que contenga un parámetro k. Los valores de k pueden enumerarse o determinarse por valor inicial, valor final y paso.
ƒ(x,k) = sin(x+k)
k de -2 a 2 en paso Pi/4
Estudio de funciones polinomiales
(Nuevo en la versión 9.0)
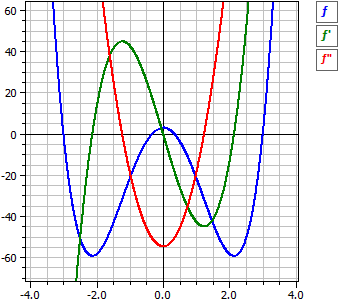
El programa realiza el análisis de una función polinomial. Esto significa que las derivadas y la antiderivada están determinadas, la función se examina para ceros, extremos, puntos de inflexión y simetría.
Función :
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Derivaciones:
¯¯¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Antiderivada:
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
Estudio de funciones racionales
(Nuevo en la versión 9.0)
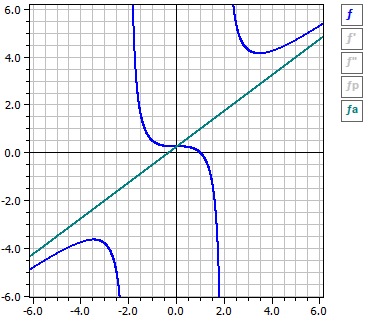
El programa realiza el análisis de una función racional (rota). Esto significa que se determinan las derivaciones y los vacíos en el dominio de definición. La función se examina para ceros, extremos, puntos de inflexión y el comportamiento de | x | → ∞.
Función:
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Singularidades:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2 Polo con cambio de signo
x =-2 Polo con cambio de signo
Derivaciones:
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = —————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ————————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
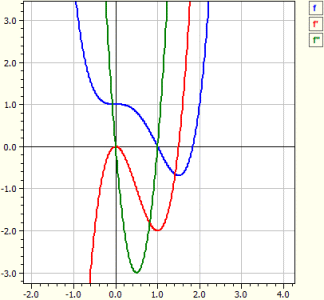
Estudio de funciones arbitrarias
El programa examina una función arbitraria ƒ. Esto significa: Se determinan las derivaciones; la función se investiga con respecto a ceros, extremos y puntos de inflexión para un rango que se había determinado de antemano; se trazan los diagramas de ƒ, ƒ y ƒ"; se emite una tabla de valores.
Función: ‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4 - 2*x^3 + 1 Estudio en el rango de -10 a 10 Derivaciones: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Los ceros: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾ N1( 1 | 0 ) m = -2 N2( 1,83929 | 0 ) m = 4,5912 Extrema: ‾‾‾‾‾‾‾‾‾‾‾‾ T1( 1,5 |-0,6875 ) m = 0 Puntos de inflexión: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1( 0 | 1 ) m = 0 W2( 1 | 0 ) m =-2
Iteración de Newton
Aproximación de los ceros de una función ƒ(x) por el método de Newton con una primera aproximación x0.
Si ingresa un valor inicial x0 que esté lo suficientemente cerca del cero que está buscando, la intersección de la tangente a la gráfica de ƒ
en el punto
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
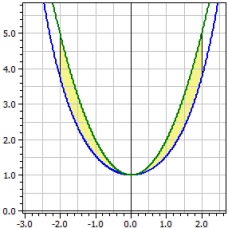
Calculo Integral
(desde febrero de 2021 con longitudes de arco)
Se calculan el contenido orientado y absoluto del área entre dos curvas de función en un intervalo deseado, es decir, las dos integrales.
También se determinan:
− los momentos de torsión para la rotación alrededor del eje x, respectivamente y,
− los cuerpos de la revolución cubiertos, y
− las longitudes de arco en el intervalo [a; b] y
− el centro de gravedad del área (si a1 = a2).
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Intervalo [a;b] de -2 a 2 Contenido orientado: A1 = -2,07961 Contenido absoluto: A2 = 2,07961 longitudes de arco: L1[a;b] = 7,254 L2[a,b] = 9,294
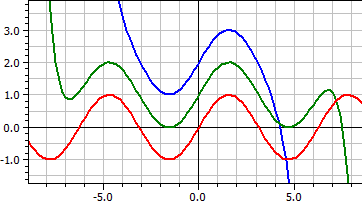
Expansión en serie
Trazador de funciones como una serie más de ƒ(x,k). Usted puede desarrollar la función con parámetros diferentes rangos y diferentes y-offset.
Los primeros 16 miembros de la serie Taylor para la función seno. ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 y 16
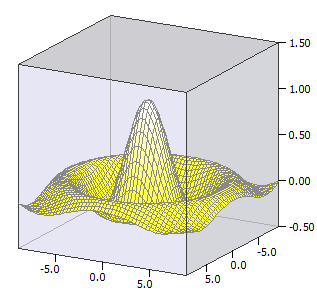
Functiones de área
Plotter de una función de área de ƒ(x,y), que puede contener una subtérmino u(x,y).
Ejemplo:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5
