MatheAss 10.0 − Stochastik
Statistik
Zu einer Urliste werden der Mittelwert (arithmetisches Mittel), der Zentralwert (Median), die Varianz und die Standardabweichung bestimmt. Zusätzlich wird die Verteilung als Histogramm und als Box-Plot ausgegegeben.
Daten:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Anzahl der Daten n = 21
Maximum max = 11
Minimum min = 1
Mittelwert x = 7,7142857
Zentralwert c = 8
Varianz s² = 6,1142857
Standardabweichung s = 2,4727082
Regression
Mit dieser Routine können Sie zu einer Messreihe eine Kurvenanpassung durchführen. Sie können zwischen folgenden Anpassungen wählen und bei Bedarf alle Punkte in x- oder y-Richtung verschieben bzw. strecken.
Ursprungsgerade ( y = a·x )
Lineare Regression ( y = a·x + b )
Polynomregression n-ter Ordnung ( y = a0 + ... + an·xn )
Geometrische Regression ( y = a·xb )
Exponentielle Regression ( y = a·bx )
Logarithmische Regression ( y = a + b·ln(x) )
Zusammen mit dem Schaubild werden der Funktionsterm der Näherungskurve, das Bestimmtheitsmaß, der Korrelationskoeffizient und die Standardabweichung ausgegeben.
Polynom-Regression
y = − 2,6299435
+ 3,8516949·x
− 0,43361582·x2
Bestimmtheitsmaß = 0,98338318
Korrelationskoeff. = 0,99165679
Standardabweichung = 0,46028731
Logistische Regression (Neu in Version 9.0)
Das Programm bestimmt zu einer Messreihe eine Kurvenanpassung an die Logistische Funktion
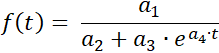
mit den Parametern
a1 = ƒ(0)·S , a2 = ƒ(0) , a3 = S - ƒ(0) ,
und a4 = -k·S und der Sättigungsgrenze S .
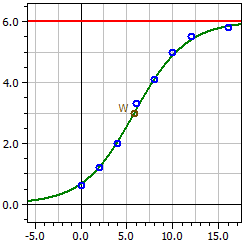
Daten aus: "Hopfenwachstum.csv"
Sättigungsgrenze: 6
Dunkelziffer: 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Wendepunkt W(5,8226/3)
Maximale Wachstumsrate ƒ'(xw) = 0,53433
8 Werte
Bestimmtheitsmaß = 0,99383916
Korrelationskoeff. = 0,99691482
Standardabweichung = 0,16172584
Kombinatorik
Berechnet werden die Anzahlen der Möglichkeiten, aus n Elementen k auszuwählen, wenn auf die Reihenfolge Wert gelegt wird oder nicht und wenn Wiederholungen zugelassen sind oder nicht.
n = 49 , k = 6 Geordnete Auswahl ohne Wiederh.= 10 068 347 520 Geordnete Auswahl mit Wiederh. = 13 841 287 201 Ungeordnete Ausw. ohne Wiederh.= 13 983 816 Ungeordnete Ausw. mit Wiederh. = 25 827 165 Permutationen von k : k ! = 720
Binomialverteilung
Berechnet werden für eine b(k;n;p) verteilte Zufallsgröße X bei festem n und festem p
- ein Stabdiagramm der Wahrscheinlichkeiten P( X = k )
- ihre numerischen Werte in einem Intervall [k-min;k-max]
- die Wahrscheinlichkeit P( k-min <= X <= k-max)
n = 50 p = 0,3
k P(X=k) P(0<=X<=k)
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
8 0,01098914 0,01825335
9 0,02197829 0,04023163
10 0,03861899 0,07885062
11 0,06018544 0,13903606
12 0,08382972 0,22286578
13 0,10501745 0,32788324
14 0,11894834 0,44683157
15 0,12234686 0,56917844
16 0,11470018 0,68387862
17 0,09831444 0,78219306
18 0,07724706 0,85944012
19 0,05575728 0,91519740
20 0,03703876 0,95223616
21 0,02267679 0,97491296
22 0,01281092 0,98772387
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
P(8<=k<=22) = 0,98045967
Hypergeometrische Verteilung
Berechnet werden für eine h(k;n;m;r) verteilte Zufallsgröße X bei bei festem n, m und festem r ein Stabdiagramm und eine Wertetabelle für die Wahrscheinlichkeiten P( X = k ).
Normalverteilung
Berechnet werden für eine N(µ,σ²) verteilte Zufallsgröße X mit gegebenem Erwartungswert µ und Varianz σ² die Dichtefunktion ƒ(x) und die Verteilungsfunktion Φ(x), das heißt das Integral über ƒ(x) .
μ = 5 σ = .75
x ƒ(x) Φ(x)
¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
2 0,00017844 0,00003167
2,33333333 0,00095649 0,00018859
2,66666666 0,00420802 0,00093192
2,99999999 0,01519465 0,00383038
3,33333332 0,04503153 0,01313415
3,66666665 0,10953585 0,03772017
3,99999998 0,21868009 0,09121120
4,33333331 0,35832381 0,18703139
4,66666664 0,48189843 0,32836063
4,99999997 0,53192304 0,49999998
5,3333333 0,48189845 0,67163934
5,66666663 0,35832383 0,81296859
5,99999996 0,21868012 0,90878878
6,33333329 0,10953586 0,96227982
6,66666662 0,04503154 0,98686585
6,99999995 0,01519465 0,99616962
7,33333328 0,00420802 0,99906808
7,66666661 0,00095649 0,99981141
7,99999994 0,00017844 0,99996833
