MatheAss 10.0 − Analysis
Folgen und Reihen (Neu in Version 9.0 ab Mai 2021)
Das Programm bestimmt die ersten n Glieder einer Folge (ai) und der zugehörigen Reihe (Summe der Folgenglieder), wenn die ersten Glieder der Folge und eine explizite Funktion ai=ƒ(i) oder eine Rekusrsionsformel ai=ƒ(a0, a1, ... , ai-1) gegeben sind.
a[0]=1; a[1]=1; a[ i ] = a[i-1] + a[i-2]; n = 20 Folge ¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Reihe ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Polynome dividieren
Das Programm berechnet das Produkt und den Quotienten von zwei Polynomen.
1. Polynom: 3·x4 - 2·x + 1
2. Polynom: 2·x + 5
Produkt: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Quotient: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Rest: 1971/16
Polynome faktorisieren (Neu in Version 9.0)
Das Programm berechnet die rationalen Nullstellen und die Linearfakorzerlegung eines Polynoms.
p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
= (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
= (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)
Rationale Nullstellen: 1/3, -1/3, 9, 3, -3
Polynome transformieren (Neu in Version 9.0)
Eine Polynomfunktion ƒ(x) kann in x-Richtung und y-Richtung verschoben oder gestreckt werden.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Verschiebung um dx = -2 , dy = 0 ƒ(x + 2) = - 1/4·x4 + 6·x2 + 1
Polynome ggT und kgV (Neu in Version 9.0 ab Februar 2021)
Das Programm berechnet den größten gemeinsamen Teiler (ggT) und das kleinste gemeinsame Vielfache (kgV) von zwei Polynomen p1(x) und p2(x).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 ggT(p1,p2) = x2 - x - 2 kgV(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
Funktionsplotter 1
Es können bis zu zehn Funktionen gleichzeitig in einem Koordinatensystem gezeichnet werden. Erlaubt sind auch Verknüpfungen oder Ableitungen von bereits definierten Funktionen.
Sei ƒ1(x)=sin(x) und ƒ2(x)=3*sqrt(x), dann ersetzt ƒ3(x)=2*y1^2-y2 ƒ3(x)=2*sin(x)^2-3*sqrt(x) ƒ4(x)=f2(y1) ƒ4(x)=3*sqrt(sin(x)) ƒ5(x)=y2' ƒ5(x)=3/(2*sqrt(x))
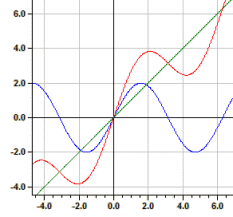
Beispiel: ƒ1(x)=sin(x), ƒ2(x)=x und ƒ3(x)=y1+y2
Funktionsplotter 2
Gezeichnet wird eine abschnittsweise definierte Funktion, die durch neun Teilfunktionen gegeben ist. Für jede der Teilfunktionen werden der Definitionsbereich, die Art des Intervalls und die Farbe eingegeben. Außerdem kann bestimmt werden, ob die Randpunkte gezeichnet werden oder nicht.
Beispiel:
Parameterkurven
Mit diesem Programm lassen sich Kurven zeichnen, die nicht durch einen expliziten Funktionsterm gegeben sind, sondern durch zwei Funktionen für die horizontale und vertikale Auslenkung.
Example: Lissajou-Figuren
x(k) = sin(3*k)
y(k) = cos(5*k)
k from -Pi to Pi
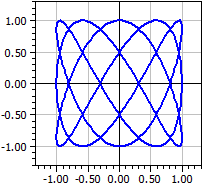
Lissajou-Figuren erhält man, wenn man an ein Oszilloskop zwei Wechselspannungen unterschiedlicher Frequenz anlegt.
Kurvenscharen
Das Programm zeichnet die Schaubilder von beliebigen Funktionen, die einen Scharparameter k enthalten. Die Werte für k können aufgelistet oder durch Anfangswert, Endwert und Schrittweite bestimmt werden.
ƒ(x,k) = sin(x+k)
k von -2 bis 2 mit Schrittweite Pi/4
Polynomfunktionen (Neu in Version 9.0)
Das Programm führt für eine ganzrationale Funktion (Polynomfunktion) die Kurvendiskussion durch. Das heißt, es werden die Ableitungen und die Stammfunktion (Aufleitung) bestimmt, die Funktion wird auf rationale Nullstellen, auf Extrema, auf Wendepunkte und auf Symmetrie untersucht.
Funktion :
¯¯¯¯¯¯¯¯
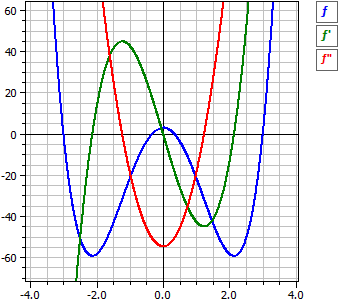
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Ableitungen :
¯¯¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Stammfunktion
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
Rationale Funktionen (Neu in Version 9.0)
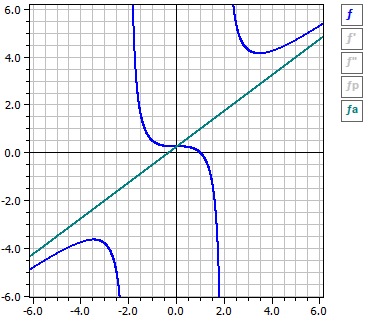
Das Programm führt für eine (gebrochen)rationale Funktion die Kurvendiskussion durch. Das heißt, es werden die Ableitungen, die Definitionslücken und die stetige Fortsetzung bestimmt. Die Funktion wird auf Nullstellen, Extrema, Wendepunkte und das Verhalten für |x|→ ∞ untersucht.
Funktion :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Definitionslücken
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2 Pol mit Vorzeichenwechsel
x =-2 Pol mit Vorzeichenwechsel
Ableitungen :
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = —————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ————————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
Kurvendiskussion
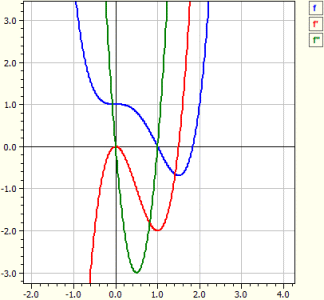
Das Programm führt für eine beliebige Funktion die Kurvendiskussion durch. Das heißt, es werden die Ableitungen bestimmt, die Funktion wird auf Nullstellen, Extrema und auf Wendepunkte untersucht, die Schaubilder von ƒ, ƒ' und ƒ" werden gezeichnet, und eine Wertetabelle wird ausgegeben.
Funktion : ‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4 - 2*x^3 + 1 Untersuchung im Bereich von -10 bis 10 Ableitungen: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Nullstellen: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾ N1( 1 | 0 ) m = -2 N2( 1,83929 | 0 ) m = 4,5912 Extrema: ‾‾‾‾‾‾‾‾‾‾‾‾ T1( 1,5 |-0,6875 ) m = 0 Wendepunkte: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1( 0 | 1 ) m = 0 W2( 1 | 0 ) m =-2
Newton-Iteration
Bei der Newton-Iteration handelt es sich um ein Näherungsverfahren zur
Berechnung einer Nullstelle von ƒ(x). Gibt man einen Startwert x0 ein, der nahe
genug an der gesuchten Nullstelle liegt, so wird als nächste Näherung
der Schnitt der Tangente an den Graph von ƒ im Punkt
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Integralrechnung
(ab Februar 2021 mit Bogenlängen)
Berechnet wird der orientierte und der absolute Inhalt der Fläche zwischen
zwei Funktionskurven in einem gewünschten Intervall. Außerdem werden
bestimmt :
- die Drehmomente bei Drehung um die x- bzw. y-Achse,
- die dabei überstrichenen Rotationsvolumen,
- die Bogenlängen im Intervall [a;b] und
- der Schwerpunkt der Fläche (wenn A1=A2).
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Integrationsintervall [a;b] von -2 bis 2 Orientierter Inhalt : A1 = -2,07961 Absoluter Inhalt : A2 = 2,07961 Bogenlängen : L1[a;b] = 7,254 L2[a,b] = 9,294
Reihenentwicklung
Gezeichnet wird eine als Reihe gegebene Funktion, wobei die Reihenentwicklungen für verschiedene Parameterbereiche verglichen und zur besseren Unterscheidung in y-Richtung versetzt werden können.
Die ersten 16 Glieder der Taylorreihe für die Sinusfunktion. ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 und 16
Flächenfunktionen
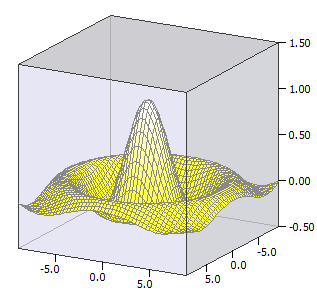
Gezeichnet wird eine Flächenfunktion ƒ(x,y), das heißt das dreidimensionale Schaubild einer Funktion mit zwei Variablen.
Beispiel:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5
