MatheAss 10.0 − Lineare Algebra
Lineare Gleichungssysteme
Das Programm bestimmt den Lösungsvektor von einem System linearer Gleichungen mit n Gleichungen und n Unbekannten.
Beispiel : Sucht man eine Parabel durch die Punkte P(1/3), Q(2/1) und R(4/9), so führt dies auf das Gleichungssystem
1·x1 + 1·x2 + 1·x3 = 3
4·x1 + 2·x2 + 1·x3 = 1
16·x1 + 4·x2 + 1·x3 = 9
L = ( 2; -8; 9 )
Die Parabel hat also die Gleichung y = 2x2 - 8x + 9.
Beispiel mit zweidim. Lösungsraum:
0·x1 + 0·x2 + 2·x3 - 1·x4 = 1
1·x1 + 1·x2 + 1·x3 + 1·x4 = 4
2·x1 + 2·x2 - 4·x3 + 5·x4 = 5
1·x1 + 1·x2 - 7·x3 + 5·x4 = 0
L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }
Lineare Optimierung
(ab Februar 2022)
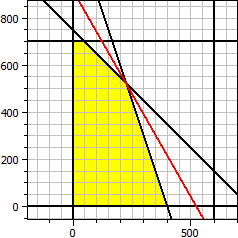
Das Programm bestimmt die optimale Lösung für eine Zielfunktion mit zwei Variablen mit linearen Ungleichungen als Randbedingungen.
Zielfunktion: ƒ(x,y) = 140·x + 80·y → Maximum Randbedingungen: x ≥ 0 y ≥ 0 x ≤ 600 y ≤ 700 x + y ≤ 750 3·x + y ≤ 1200 Maximum x = 225 y = 525 ƒ(x,y) = 73500
Linearkombination
Das Programm bestimmt die Linearkombination eines Vektors aus drei gegebenen Vektoren. Die Routine eignet sich auch dazu, die lineare Unabhängigkeit von drei Vektoren im Raum zu prüfen, das heißt, ob sie in einer Ebene liegen.
⎧ 1 ⎫ ⎧ 2 ⎫ ⎧ 0 ⎫ ⎧ 2 ⎫
a·⎪ 2 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭ ⎩ 0 ⎭ ⎩ 7 ⎭
Lösung :
a = -12 b = 7 c = 20
Skalarprodukt
Das Programm berechnet zu zwei Vektoren deren Skalarprodukt, die Länge der beiden Vektoren und den eingeschlossenen Winkel.
-> ⎧ 1 ⎫ -> ⎧ 5 ⎫
a = ⎪ 3 ⎪ b = ⎪ 0 ⎪
⎩ 1 ⎭ ⎩ 3 ⎭
Skalarprodukt der Vektoren = 8
Länge des ersten Vektors = √11 = 3,3166248
Länge des zweiten Vektors = √34 = 5,8309519
eingeschlossener Winkel α = 65,564402°
Vektorprodukt
Das Programm berechnet zu zwei Vektoren das Vektorprodukt, sowie seinen Betrag. Das Vektorprodukt steht auf dem von ihnen aufgespannten Parallelogramm senkrecht, und sein Betrag ist gleich dem Flächeninhalt des Parallelogramms.
-> ⎧ 1 ⎫ -> ⎧ 7 ⎫
a = ⎪ 2 ⎪ b = ⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 4 ⎭
-> -> ⎧ 5 ⎫ -> ->
a x b = ⎪ 17 ⎪ |a x b|= √483 = 21,977261
⎩-13 ⎭
Spatprodukt
Das Programm berechnet zu drei Vektoren das Spatprodukt. Sein Betrag gibt dasVolumen des verschobenen Quaders (Spat) an, der von den drei Vektoren aufgespannt wird.
-> ⎧ 2 ⎫ -> ⎧ 2 ⎫ -> ⎧ 3 ⎫
a = ⎪ 3 ⎪ b = ⎪-1 ⎪ c = ⎪ 9 ⎪
⎩ 5 ⎭ ⎩ 7 ⎭ ⎩ 2 ⎭
-> -> ->
( a x b ) · c = 26
Matrizeninversion
Das Programm berechnet zu einer quadratischen Matrix der Ordnung n die Determinante, den Rang und die inverse Matrix.
Matrix: ⎧ 0 1 1 ⎫ ⎪ 0 1 3 ⎪ ⎩ 2 0 1 ⎭ Inverse Matrix ⎧ 0,25 -0,25 0,5 ⎫ ⎪ 1,5 -0,5 0 ⎪ ⎩ -0,5 0,5 0 ⎭ Ordnung = 3, Rang = 3, Determinante = 4
Pseudoinverse Matrix
Sind die Spalten einer Matrix A linear unabhängig, so ist
A+ = ( AT· A )-1· AT
Dabei ist A+ eine Linksinverse von A ,
das heißt es gilt:
Matrix A ¯¯¯¯¯¯¯¯ ⎧ 1 1 1 1 ⎫ ⎩ 5 7 7 9 ⎭ AT· A ¯¯¯¯¯ ⎧ 26 36 36 46 ⎫ ⎪ 36 50 50 64 ⎪ ⎪ 36 50 50 64 ⎪ ⎩ 46 64 64 82 ⎭ AT· A nicht invertierbar A · AT ¯¯¯¯¯¯ ⎧ 4 28 ⎫ ⎩ 28 204 ⎭ ( A · AT )-1 ¯¯¯¯¯¯¯¯¯¯¯ ⎧ 6,375 -0,875 ⎫ ⎩ -0,875 0,125 ⎭ Rechtsinverse: AT · ( A · AT )-1 ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 2 -0,25 ⎫ ⎪ 0,25 0 ⎪ ⎪ 0,25 0 ⎪ ⎩ -1,5 0,25 ⎭
Matrizenmultiplikation
Das Programm berechnet zu zwei Matrizen die Produktmatrix.
1. Matrix 2. Matrix ⎧ 1 2 3 0 ⎫ ⎧ 1 2 3 4 ⎫ ⎪ 4 5 6 0 ⎪ ⎪ 5 6 7 8 ⎪ ⎪ 0 0 0 0 ⎪ ⎪ 9 10 11 12 ⎪ ⎩ 0 0 0 0 ⎭ ⎩ 0 0 0 0 ⎭ Produktmatrix ⎧ 38 44 50 56 ⎫ ⎪ 83 98 113 128 ⎪ ⎪ 0 0 0 0 ⎪ ⎩ 0 0 0 0 ⎭
