MatheAss 10.0 − 2-dim. Geometry
Rectangular Triangles
If two properties of a rectangular triangle are given, the program calculates the others.
Given:
¯¯¯¯¯¯
Hypot. segment p = 1,8
Area A = 6
Results :
¯¯¯¯¯¯¯
Cathete a = 3
Cathete b = 4
Hypotenuse c = 5
Angle α = 36,869898°
Angle β = 53,130102°
Hypot. segment q = 3,2
Altitude h = 2,4
Triangles by three Elements
Given three outer properties (sides or angles) of a triangle, the program calculates the sides, the angles, the altitudes, the medians and the angle bisectors, the perimeter and the area, as well as the centers and the radii of the incircle and the circumcircle.
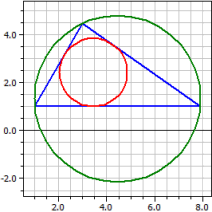
.Given: a=6, b=4 and α=60°
Vertices : A(1|1) B(7,899|1) C(3|4,4641)
Sides : 6 4 6,89898
Angles : 60° 35,2644° 84,7356°
Altitudes : 3,98313 5,97469 3,4641
Medians : 4,77472 6,148 3,75513
Bisectr. : 4,38551 6,11664 3,5464
Circumcir.: M(4,44949|1,31784) ru = 3,4641
Incircle : O(3,44949|2,41421) r i = 1,41421
Area : A = 11,9494 Perimeter : u = 16,899
 Triangles of three Points
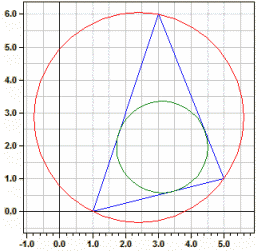
Triangles of three Points
From the coordinates of three vertices, the program calculates all outer and inner properties (see Triangles by three elements ).
Vertices : A(1|0) B(5|1) C(3|6)
Sides : 5,38516 6,32456 4,12311
Angles : 57,5288° 82,2348° 40,2364°
Altitudes : 4,0853 3,47851 5,33578
Medians : 4,60977 3,60555 5,5
Bisectr. : 4,37592 3,51849 5,46225
Circumcir.: M(2,40909|2,86364) ru = 3,19154
Incircle : O(3,11866|1,96195) r i = 1,38952
Area : A = 11 Perimeter : u = 15,8328
 Special Straight Lines in a Triangle (New in version 9.0)
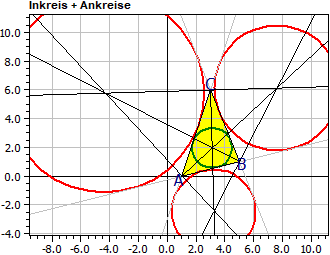
Special Straight Lines in a Triangle (New in version 9.0)
The program determines the equations of the perpendicular bisectors, of the medians, of the angle bisectors and of the altitudes of a triangle. In addition, the centers and radii of the circumcircle, the incircle, the three excircles and the nine-point circle (since march 2025).
.Given:
¯¯¯¯¯¯
Vertices: A(1|0) B(5|1) C(3|6)
Results:
¯¯¯¯¯¯¯
Sides: a : 5·x + 2·y = 27
b : 3·x - y = 3
c : x - 4·y = 1
Incircle: Mi(3,119|1,962) r i = 1,390
Excircles: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
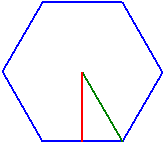
 Regular Polygons
Regular Polygons
If the number of corners and one of the following sizes are given, the program calculates the others.
Side a, incircle radius ri, circumcircle radius rc, perimeter u or area A.

Given:
¯¯¯¯¯¯
Vertices n = 6
Circumcircle rc = 1
Results:
¯¯¯¯¯¯¯
Side a = 1
Incircle ri = 0,8660254
Perimeter p = 6
Area A = 2,5980762
 Arbitrary Polygons
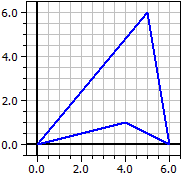
Arbitrary Polygons
From the coordinates of the vertices of a polygon, the program calculates the area, the perimeter, the centroid of vertices and the centroid of area.
Vertices: Area A = 18
A(0|0)
B(4|1) Perimeter p = 22,032567
C(6|0)
D(5|7) Centroid of vertices:
CV(3,75|2)
Centroid of area:
CA(3,72222|2,66667)
 Mappings of Polygons
(revised in version 9.0)
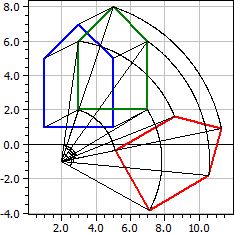
Mappings of Polygons
(revised in version 9.0)
The program makes it possible to apply a concatenation of mappings to a polygon. You can choose from displacement, straight reflection, point reflection, rotation, centric stretching and shear.
Original polygon A(1|1), B(5|1), C(5|5), D(3|7), E(1|5), 1. Translation: dx=2, dy=1 ☑ A(3|2), B(7|2), C(7|6), D(5|8), E(3|6), 2. Rotation: Z(2|-1), α=-60° ☑ A(5,0981|-0,36603), B(7,0981|-3,8301), C(10,562|-1,8301), D(11,294|0,90192), E(8,5622|1,634),
 Circular Sections
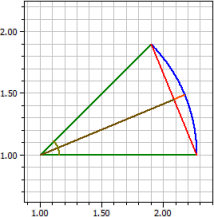
Circular Sections
If two of the following sizes are given, the program calculates the others.
Given:
¯¯¯¯¯¯
Arc b = 1
Angle α = 45°
Results:
¯¯¯¯¯¯¯
Radius r = 1,2732395
Chord s = 0,97449536
Section A1 = 0,63661977
Distance d = 1,17632
Arrow height h = 0,096919589
Segment A2 = 0,063460604
Area A = 5,0929582
Perimeter p = 8
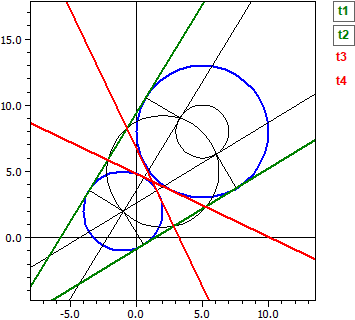
 Tangent Lines to Circles (New in version 9.0 from February 2021)
Tangent Lines to Circles (New in version 9.0 from February 2021)
- The tangent to a circle k in a point B
- The tangents to a circle k through a point P outside the circle
- The tangents to a circle k parallel to a straight line g
- The tangents on two circles k1 and k2
Given: ¯¯¯¯¯ k1 : M(5|8) , r=5 k2 : M(-1|2) , r=3 Outer tangents ¯¯¯¯¯¯¯¯¯¯¯¯ t1: -4,2923·x + 7,04104·y = -6,36427 t2: -7,04104·x + 4,29230·y = 40,3643 Inner tangents ¯¯¯¯¯¯¯¯¯¯¯¯ t3: 1,21895·x + 2,55228·y = 12,3709 t4: -2,55228·x - 1,21895·y = -8,3709
 Intersections in the Plane
Intersections in the Plane
The program calculates the intersections of straight lines and circles
Two Straights
g : x + y = 0 h : x - y = 5 Intersection point : S(2,5|-2,5) Intersection angle : 90° Distances from origin : d(g,O) = 0 d(h,O) = 3,5355339
Straight and Circle
Circle and line : ¯¯¯¯¯¯¯¯¯¯¯¯¯ k : M(5|0) r = 5 g : x + y = 0 Intersection points : ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ S1(5|-5) S2(0|0)
Two Circles
Given are the circles : ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ k1 : M1(5|5) r1 = 5 k2 : M2(0|0) r2 = 5 Intersection points : ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ S1(5|0) S2(0|5) Connecting line : ¯¯¯¯¯¯¯¯¯¯¯¯¯ x + y = 5