Dreiecke aus drei Größen
Dreiecke werden durch drei äußere Größen ( Seiten oder Winkel ) eindeutig bestimmt, wenn einer der Kongruenzsätze erfüllt ist:
- sss drei Seiten sind gegeben.
- sww eine Seite und zwei Winkel sind gegeben.
- sws zwei Seiten und der eingeschlossene Winkel sind gegeben.
- Ssw zwei Seiten und der Winkel, der der größeren gegenüberliegt, sind gegeben.
In diesen Fällen berechnet das Programm die Seiten, die Winkel, die Höhen, die Seiten- und die Winkelhalbierenden (Strecken von der Ecke bis zum Schnittpunkt mit der Seite gegenüber), den Umfang und den Flächeninhalt, sowie die Mittelpunkte und Radien von Inkreis und Umkreis des Dreiecks.
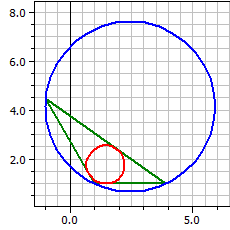
Außerdem wird das Dreieck mit In- und Umkreis gezeichnet.
Gibt man zwei Seiten und den Winkel ein, der der kleineren Seite gegenüberliegt (sSw), gibt es meist keine eindeutige oder gar keine Lösung. Im ersten Fall werden beide Lösungen angezeigt.
Beispiel 1:
Gegeben: a=6, b=4 und α=60°
Ecken: A(1|1) B(7,899|1) C(3|4,4641)
Seiten: 6 4 6,89898
Winkel: 60° 35,2644° 84,7356°
Höhen: 3,98313 5,97469 3,4641
Seitenh.: 4,77472 6,148 3,75513
Winkelh.: 4,38551 6,11664 3,5464
Umkreis: M(4,44949|1,31784) ru = 3,4641
Inkreis: O(3,44949|2,41421) ri = 1,41421
Fläche: A = 11,9494 Umfang : u = 16,899

Beispiel 2:
Gegeben: a = 6, b = 4, β = 35,2644
1. Lösung:
Ecken: A(1|1) B(7,899|1) C(3|4,464)
Seiten: 6 4 6,89898
Winkel: 60° 35,2644° 84,7356°
Höhen: 3,98313 5,97469 3,46410
Seitenh.: 4,77472 6,14800 3,75513
Winkelh.: 4,38550 6,11664 3,5464
Umkreis: M(4,449|1,3178) ru = 3,4641
Inkreis: O(3,449|2,4142) r i = 1,41421
Fläche: A = 11,9494 Umfang u = 16,899
—————————————————————
2. Lösung:
Ecken: A(1|1) B(3,899|1) C(-1|4,464)
Seiten: 6 4 2,89898
Winkel: 120° 35,2644° 24,7356°
Höhen: 1,67373 2,51059 3,46410
Seitenh.: 1,78943 4,26639 4,88866
Winkelh.: 1,68082 3,72554 4,68861
Umkreis: M(2,449|4,146) ru = 3,4641
Inkreis: O(1,449|1,779) r i = 0,7785
Fläche: A = 5,0212 Umfang u = 12,899