Studio di funzioni arbitrarie

Il programma esegue il studio di una funzione arbitraria. Ciò significa che determina i derivati, i valori nulli, gli estremi e i punti di inversione in un determinato dominio. Vengono disegnati i diagrammi di f, f' e f" e viene calcolata una tabella di valori.

Inserimento di funzioni

Oltre ai termini di funzione, vengono inseriti il ​​campo di studio, la precisione dello studio e la modalità angolare

Il campo di studio è l'intervallo in cui vengono ricercati i valori null, extrema e i punti di inversione della funzione. Non dovremmo sceglierlo troppo grande, perché allo stesso tempo cresce il passo con cui si cercano le inversioni del segno della funzione.

Uscita derivati

I derivati ​​f' e f" di f sono determinati dalla derivazione simbolica dopo le consuete regole di detrazione. In caso di problemi, è possibile disattivare i derivati. Il resto della discussione sulla curva si svolge quindi numericamente. I quozienti differenziali df(x)/dx sono sostituiti dai quozienti di differenzi Δf(x)/Δx con un piccolo Δx.

Gli output sono i null, i massimi relativi, i minimi relativi e i punti di inversione della funzione nel campo di studio.

Le lacune nell'area di definizione non vengono riconosciute. Sebbene non rientrino nell'intervallo numerico dell'aritmetica binaria o vengono ignorati. Per questo motivo, estremi o punti di inversione potrebbero essere emersi con disprezzo.

Ciò che viene detto delle lacune nel campo della definizione vale anche per la continuità e l'esistenza di una derivata di f, f' e f". Rimane naturalmente una parte del tuo lavoro per te.

Esempio:

Funzione:
‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ(x) = x^4 - 2*x^3 + 1
  Studio nella gamma da -10 a 10

Derivati:
‾‾‾‾‾‾‾‾‾‾‾
  ƒ'(x) = 4*x^3-6*x^2
  ƒ"(x) = 12*x^2-12*x

Zeri:
‾‾‾‾‾‾
  N1( 1 | 0 )                  m = -2
  N2( 1,83929 | 0 )       m =  4,5912

Estremi:
‾‾‾‾‾‾‾‾‾‾‾
  T1( 1,5 |-0,6875 )      m = 0

Punti di flesso:
¯¯¯¯¯¯¯¯¯¯¯¯
  W1( 0 | 1 )                 m = 0
  W2( 1 | 0 )                 m =-2

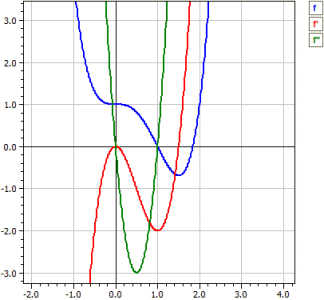
Esci dalla tabella dei valori:

Qui possiamo determinare l'intervallo e il passo, con cui verrà calcolata la tabella dei valori di f, f 'e f ". Per l'intervallo viene proposto il campo di studio. Posizioni in cui la funzione non è definita sono contrassegnati con ---.

Vedi anche:

Note sulla procedura | Funzioni supportate | Impostazioni delle grafiche