Linee speciali in un triangolo

Se vengono inserite le coordinate dei tre vertici di un triangolo, il programma calcola le equazioni delle asse dei lati[1], delle mediane[2], delle bisettrici angolari[3] e delle altezze[4]. Inoltre, i centri e i raggi del circumcerchio[5], del incerchio[6], dei tre excerchi[7] e del cerchio di Feuerbach[8].

Un elenco di check boxes può essere utilizzato per selezionare quali oggetti devono essere calcolati e disegnati.

Asse dei lati
Mediane
Bisettrici
Altezze
Incerchio
Circumcerchio
Excerchi
Cerchio di Feuerbach

Esempio 1: Il incerchio ed i excerchi di un triangolo 

Dato:  
¯¯¯¯      
          Vertici: A(1|0)  B(5|1)  C(3|6)
     
Risultati:       
¯¯¯¯¯¯¯  
            Lati: a:  5 · x + 2y = 27       
                    b:  3x - y = 3       
                    c:  x - 4y = 1     
	       
    Incerchio: Mi(3.119|1.962)    ri = 1.390
	    
     Excerchi: Ma(7.626|6.136)   ra = 4.346
                     Mb(-4.356|5.784)  rb = 6.910
                     Mc(3.248|-2.427)  rc = 2.900

Il centro del incerchio (verde) si trova sulla bisettrice dei tre angoli interni. I centri dei excerchi (rosso) sono ciascuno sulla bisettrice di un angolo interno e sulla bisettrice dell'angolo esterno degli altri due angoli del triangolo. Queste linee di costruzione sono anche disegnate.

Esempio 2: Le altezze in un triangolo ad angolo ottuso 

Dato:  
¯¯¯¯    
          Vertici: A(7|3)  B(16|10)  C(8|9)        
     
Risultati:       
¯¯¯¯¯¯¯
         Lati: a: -x + 8y = 64       
                 b: 6x -  y = 39   
                 c: 7x - 9y = 22  
      
   Altezze: ha: 8x + y = 59    
                 hb: x + 6y = 76    
                 hc: 9x + 7y = 135  
				 
Punti a piombio:  Ha(6,277|8,785)   Hb(8,378|11,27)
      
       Orthocentro: H(11.05|8.26)

L'intersezione delle altezze di un triangolo ottuso si trova al di fuori del triangolo. Vengono tracciate anche le linee di costruzione. Per renderli più visibili, le linee della griglia sono state nascoste.

Esempio 3: Gli excerchi et il cerchio di Feuerbach

Dato:  
¯¯¯¯ 
                 Vertici:  A(1|0)   B(5|1)   C(3|6)
 
Risultati:       
¯¯¯¯¯¯¯
                   Lati:   a :  5·x + 2·y = 27
                             b :  3·x − y = 3
                             c :  x − 4·y = 1
 
            Excerchi:  Ma(7,626|6,136)     ra = 4,346
                             Mb(-4,356|5,784)    rb = 6,910
                             Mc(3,248|-2,427)    rc = 2,900

Cerchio di Feuerbach: M9(3,295|2,068)   r9 = 1,596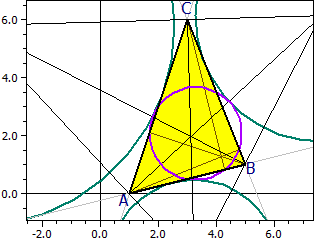


Il cerchio di Feuerbach tocca il incerchio e gli excerchi (teorema di Feuerbach).

Vedi anche:

Impostazioni delle grafiche
Wikipedia: Excerchi | Cerchio di Feuerbach

[1]  Le asse dei lati sono le linee rette, che intersecano verticalmente un lato del triangolo al suo centro. Il loro punto di intersezione è il centro del perimetro.
[2]  Le mediane sono i segmenti di linea da un bordo del triangolo al centro del lato opposto. Il loro punto di intersezione è il baricentro del triangolo.
[3]  Le bisettrici angolari, come suggerisce il loro nome, dimezzano uno degli angoli interni del triangolo. Il loro punto di intersezione è il centro dell'incircolo del triangolo.
[4]  Le altezze sono le linee perpendicolari da un vertice del triangolo al lato opposto. Il loro punto di intersezione è chiamato ortocentro del triangolo.
[5]  Il circumcerchio di un triangolo è il cerchio attraverso i bordi del triangolo. In un triangolo ad angolo acuto, il suo centro si trova all'interno, in un triangolo ad angolo ottuso si trova al di fuori del triangolo.
[6]  Il incerchio è il cerchio che tocca i tre lati del triangolo dall'interno. Il suo centro è l'intersezione delle bisettrici angolari.
[7]  Gli excerchi toccano un lato del triangolo dall'esterno e sono toccati tangenzialmente dalle estensioni degli altri due lati.
[8]  Il cerchio di Feuerbach è anche noto come il cerchio dei nove punti; infatti oltre a contenere i punti medi dei lati, i piedi delle sue altezze e i punti medi dei segmenti compresi fra i vertici e l'ortocentro.