Tangents to circles - Construction

The legend on the right-hand side of the graphic serves not only to distinguish the tangents by color, but also as a switch to show or to hide the construction lines.

The tangent to a circle k at a point B.

The basis for the construction is that the tangent of a circle is perpendicular to the contact radius. So you can draw the straight line through M and B and construct the perpendicular straight line through B.

 

The tangents to a circle k through a point P outside the circle

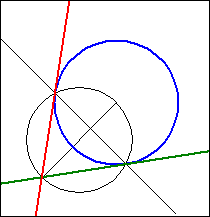
The points of contact B₁ and B₂ of the tangents are obtained as the points of intersection of the Thales circle over the segment MP with the circle k.
The straight lines (PB₁) and (PB₂) are the desired tangents.

The additional line (B₁ B₂) is the polar of P, which we used to calculate the tangent equations.

 

The tangents to a circle k parallel to a straight line g

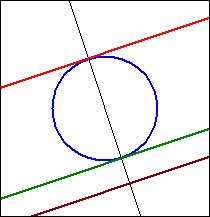
The points of contact B₁ and B₂ of the tangents are obtained as intersections of the perpendicular line from M to g with the circle k.
The parallels to g through  B₁  and  B₂  are the desired tangents.

 

The common tangents to two circles k₁ and k₂

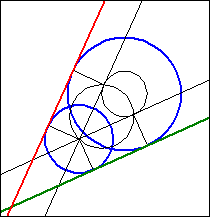
In order to construct the outer tangents to two circles k₁ (M₁ , r₁ ) and k₂ (M₂ , r₂ ), one first draws a circle  k₃  around  M₁  with radius  r₃=r₁−r₂.
Its intersection points  S₁  and  S₂  with the Thales circle over  M₁M₂  are the points of contact of two tangents that can be placed from  M₂  to the circle  k₃.
The half lines from  M₁  through  S₁  and  S₂  resp. intersect the circle  k₁  at the points of contact of the sought outer tangents. These are parallel to the tangents to the auxiliary circle  k₃.

 

If  k₂ is completely outside of  k₁, there are also two "inner" tangents that cross between the circles.
To construct the inner tangents to the two circles  k₁(M₁,r₁)  and  k₂(M₂,r₂), first draw a circle  k₃  around  M₁  with a radius  r₃=r₁+r₂.
Its intersection points  S₁  and  S₂  with the Thales circle over  M₁M₂  are the contact points of two tangents that can be placed from  M₂  onto the circle  k₃.
The half-straight lines from  M₁  through  S₁  and  S₂ resp. intersect the circle  k₁  at the points of contact of the inner tangents sought. These are parallel to the tangents to the auxiliary circle  k₃.

See also:

Setting the graphics
Wikipedia: Tangent_lines to circles | Pole and polar