Lineare Gleichungssysteme

Das Programm bestimmt den Lösungsvektor von einem System linearer Gleichungen (LGS) mit n Gleichungen und n Unbekannten. Eingegeben werden der Grad n und die Koeffizienten des Gleichungssystems, das zuvor auf folgende Form gebracht werden muss:

a_1,1 ·x₁ + ... + a_1,n ·x_n = b₁

  ⋮                                  ⋮

a_n,1 ·x₁ + ... + a_n,n ·x_n = b_n

Als Zwischenergebnis kann man sich die ref (Row Echelon Form = Dreiecksform) und die rref (Reduced Row Echelon Form = Diagonalform) der Koeffizientenmatrix ausgeben lassen.

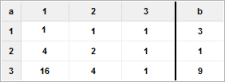
Beispiel mit eindeutiger Lösung:

 1·x1 + 1·x2 + 1·x3  =   3
 4·x1 + 2·x2 + 1·x3  =   1
16·x1 + 4·x2 + 1·x3  =   9

L = { ( 2; -8; 9; ) }

Beispiel mit eindim. Lösungsraum:

 2·x1 + 3·x2 + 4·x3  =   0
 1·x1 - 1·x2 - 1·x3  =   1
 3·x1 + 2·x2 + 3·x3  =   1

L = { ( 0,6-0,2t; -0,4-1,2t; t ) | t ∈ R }}

Beispiel mit zweidim. Lösungsraum

 0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
 1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
 2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
 1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Anwendung zum ersten Beispiel:

Sucht man eine Parabel durch die Punkte P(1|3), Q(2|1) und R(4|9), so führt dies auf folgendes Gleichungssystem

Ansatz:   ƒ(x) = a·x² + b·x + c

Das Gleichungssystem hat den Lösungsvektor:     (2, -8, 9)

Die Parabel hat also die Gleichung  y = 2x² - 8x + 9.

Popup-Menü:

Mit der rechten Maustaste öffnen sie ein Kontextmenü, das Ihnen die folgenden Funktionen für die Koeffizienten-Matrix anbietet.

• Matrix ausschneiden, Matrix kopieren und Matrix einfügen

  Damit kann die Matrix über die Zwischenablage etwa in die Matrizenmultiplikation kopiert werden.

• Matrix exportieren bzw. Matrix importieren

  Exportiert bzw. importiert wird im CSV-Format (Comma separated values), mit dem Daten mit einer Excel-Datei ausgetauscht werden können.

Siehe auch:

Wikipedia: Lineares Gleichungssystem